
若有穷数列 ,
,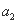 ,
, ,
, (
(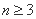 )满足:(1)
)满足:(1) ;(2)
;(2)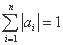 .
.
则称该数列为“ 阶非凡数列”.
阶非凡数列”.
(Ⅰ)分别写出一个单调递增的“ 阶非凡数列”和一个单调递减的“
阶非凡数列”和一个单调递减的“ 阶非凡数列”;
阶非凡数列”;
(Ⅱ)设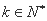 ,若“
,若“ 阶非凡数列”是等差数列,求其通项公式;
阶非凡数列”是等差数列,求其通项公式;
(Ⅲ)记“ 阶非凡数列”的前
阶非凡数列”的前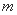 项的和为
项的和为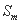 (
(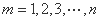 ),证明:
),证明:
(1)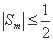 ; (2)
; (2) .
.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
下列关于命题的说法中正确的是________.
①对于命题p:∃x∈R,使得x2+x+1<0,则綈p:∀x∈R,均有x2+x+1≥0
②“x=1”是“x2-3x+2=0”的充分不必要条件
③命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”
④若p∧q为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在公路 的两侧有四个村镇:
的两侧有四个村镇: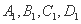 ,它们通过小路和公路相连,各路口
,它们通过小路和公路相连,各路口
分别是 . 某燃气公司要在公路旁建一个调压站,并从调压站出发沿公路和各小路通过低压输配管道(每个村镇单独一条管道)将燃气送到各村镇,为使低压输配管道总长度
. 某燃气公司要在公路旁建一个调压站,并从调压站出发沿公路和各小路通过低压输配管道(每个村镇单独一条管道)将燃气送到各村镇,为使低压输配管道总长度
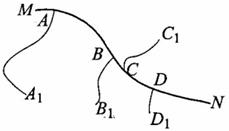
最小,调压站应建在
A. 处 B.
处 B. 段公路旁的任一处
段公路旁的任一处
C. 处 D.
处 D.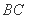 段公路旁的任一处
段公路旁的任一处
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两定点F1(-1,0) 、F2(1,0), 则命题甲: 是
是 与
与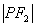 的等差中项,命题乙:动点P的轨迹是椭圆,则甲是乙的 ( ).
的等差中项,命题乙:动点P的轨迹是椭圆,则甲是乙的 ( ).
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.非充分非必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com