Question

11．设点M（1，m），若在圆O：x²+y²=1上存在一点N，使得∠OMN=30°，则实数m的取值范围是[-$\sqrt{3}$，$\sqrt{3}$]．

Answer 1

分析 根据题意，问题转化为直线x=1上的点M与圆x²+y²=1上的点T（1，0）所组成的∠OMT≥30°，由此求出m的取值范围．

解答 解：如图所示，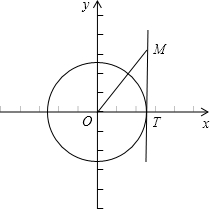
易知M（1，m）在直线x=1上，设圆x²+y²=1与直线x=1的交点为T，
假设存在点N，使得∠OMN=30°，则必有∠OMN≤∠OMT，
所以要是圆上存在点N，使得∠OMN=30°，只需∠OMT≥30°，
因为T（1，0），所以只需在Rt△OMT中，tan∠OMT=$\frac{OT}{TM}$=$\frac{1}{|m|}$≥tan30°=$\frac{\sqrt{3}}{3}$，
解得|m|≤$\sqrt{3}$，当m=0时，满足题意，
故m∈[-$\sqrt{3}$，$\sqrt{3}$]．
故答案为：[-$\sqrt{3}$，$\sqrt{3}$]．

点评 本题考查了直线与圆的应用问题，解题时应弄清楚M点所在的位置，找到∠OMN与∠OMT的大小关系，从而构造出关于m的不等式，是基础题目．