
| A. | 4x-3y-16=0或4x-3y+16=0 | B. | 4x-3y-16=0或4x-3y+24=0 | ||
| C. | 4x-3y+16=0或4x-3y+24=0 | D. | 4x-3y+16=0或4x-3y-24=0 |
分析 利用两点间的距离公式可得|AB|,利用三角形的面积,求出C到AB的距离,即可求出顶点C的轨迹方程.
解答 解:∵A(-1,0),B(2,4),
∴得|AB|=$\sqrt{{(2+1)}^{2}+{(4-0)}^{2}}$=5,
∵△ABC的面积为10,∴动点C到AB的距离为4.
设C(x,y),AB的方程为:$\frac{y-4}{x-2}=\frac{4-0}{2+1}$,即4x-3y+4=0.
由题意可得:$\frac{\left|4x-3y+4\right|}{\sqrt{{4}^{2}+{(-3)}^{2}}}=4$,
即|4x-3y+4|=20,动点C的轨迹方程为:4x-3y-16=0或4x-3y+24=0
故选:B
点评 本题考查轨迹方程的求法,点到直线的距离公式的应用.利用三角形的面积,求出C到AB的距离是解决本题的关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
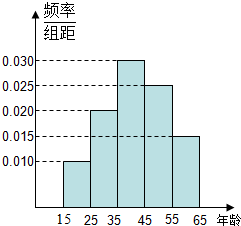 为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.
为了了解四川省各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“四川省有哪几个著名的旅游景点?”统计结果如表.| 组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.5 |
| 第2组 | [25,35) | 18 | x |
| 第3组 | [35,45) | b | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65] | 3 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
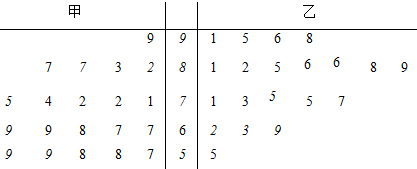
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 | 40 |
| P(χ2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 理科 | 文科 | |
| 男 | 14 | 10 |
| 女 | 6 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数分值 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150) |
| 文科频数 | 2 | 4 | 8 | 3 | 3 |
| 理科频数 | 3 | 7 | 12 | 20 | 8 |
 | 文科 | 理科 |
| 概念 | 15 | 30 |
| 其它 | 5 | 20 |
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com