
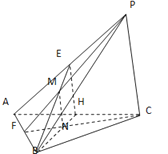
【题目】如图,在三棱锥![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,E、F、H分别为AP、AB、AC的中点,PF交BE于点M,CF交BH于点N,
,E、F、H分别为AP、AB、AC的中点,PF交BE于点M,CF交BH于点N,![]() ,
,![]() .
.
![]() 求证:
求证:![]() 平面BEH;
平面BEH;
![]() 求证:
求证:![]() ;
;
![]() 求直线PA与平面ABC所成角的正弦值.
求直线PA与平面ABC所成角的正弦值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() 。
。
【解析】
(1)推导出BH⊥AC,EH⊥AC,由此能证明AC⊥平面BEH.
(2)推导出N是△ABC的重心,M是△ABP的重心,从而![]() ,由此能证明PC∥MN.
,由此能证明PC∥MN.
(3)取BH的中点G,连结AG,推导出EG⊥BH,EG⊥AC,EG⊥平面ABC,从而∠EAG是PA与平面ABC所成角,由此能求出直线PA与平面ABC所成角的正弦值.
证明:![]() 是边长为2的正三角形,H是AC中点,
是边长为2的正三角形,H是AC中点,
![]() ,
,
![]() ,E、H分别为AP、AC的中点,
,E、H分别为AP、AC的中点,
![]() ,
,![]() ,
,
![]() ,
,![]() 平面BEH.
平面BEH.
证明:![]() 交BE于点M,CF交BH于点N,
交BE于点M,CF交BH于点N,
![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,E、F、H分别为AP、AB、AC的中点,
,E、F、H分别为AP、AB、AC的中点,
![]() 是
是![]() 的重心,
的重心,![]() ,M是
,M是![]() 的重心,
的重心,![]() ,
,
![]() ,
,![]() .
.
![]() 取BH的中点G,连结AG,
取BH的中点G,连结AG,
![]() ,
,![]() ,
,
![]() 平面BEH,
平面BEH,![]() ,
,![]() 平面ABC,
平面ABC,
![]() 是PA与平面ABC所成角,
是PA与平面ABC所成角,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() 直线PA与平面ABC所成角的正弦值为
直线PA与平面ABC所成角的正弦值为![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,棱长为2,M,N分别为A1B,AC的中点.
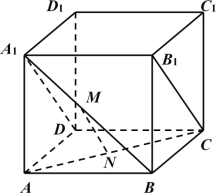
(1)证明:MN//B1C;
(2)求A1B与平面A1B1CD所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 与圆
与圆![]() :
:![]() 相切,并且椭圆
相切,并且椭圆![]() 上动点与圆
上动点与圆![]() 上动点间距离最大值为
上动点间距离最大值为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,
,![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,求
,求![]() 面积的最大值,并求取得最大值时直线
面积的最大值,并求取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市面上有某品牌![]() 型和
型和![]() 型两种节能灯,假定
型两种节能灯,假定![]() 型节能灯使用寿命都超过5000小时,经销商对
型节能灯使用寿命都超过5000小时,经销商对![]() 型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:
型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:

某商家因原店面需要重新装修,需租赁一家新店面进行周转,合约期一年.新店面需安装该品牌节能灯5支(同种型号)即可正常营业.经了解,![]() 型20瓦和
型20瓦和![]() 型55瓦的两种节能灯照明效果相当,都适合安装.已知
型55瓦的两种节能灯照明效果相当,都适合安装.已知![]() 型和
型和![]() 型节能灯每支的价格分别为120元、25元,当地商业电价为0.75元/千瓦时.假定该店面一年周转期的照明时间为3600小时,若正常营业期间灯坏了立即购买同型灯管更换.(用频率估计概率)
型节能灯每支的价格分别为120元、25元,当地商业电价为0.75元/千瓦时.假定该店面一年周转期的照明时间为3600小时,若正常营业期间灯坏了立即购买同型灯管更换.(用频率估计概率)
(Ⅰ)根据频率直方图估算![]() 型节能灯的平均使用寿命;
型节能灯的平均使用寿命;
(Ⅱ)根据统计知识知,若一支灯管一年内需要更换的概率为![]() ,那么
,那么![]() 支灯管估计需要更换
支灯管估计需要更换![]() 支.若该商家新店面全部安装了
支.若该商家新店面全部安装了![]() 型节能灯,试估计一年内需更换的支数;
型节能灯,试估计一年内需更换的支数;
(Ⅲ)若只考虑灯的成本和消耗电费,你认为该商家应选择哪种型号的节能灯,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
(1)甲不在两端;
(2)甲、乙相邻;
(3)甲、乙、丙三人两两不得相邻;
(4)甲不在排头,乙不在排尾。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切,圆心在
相切,圆心在![]() 轴上,且直线
轴上,且直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率乘积为
的斜率乘积为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com