
【题目】已知函数f(x)=loga ![]() (a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(1)求f(0)的值和实数m的值;
(2)当m=1时,判断函数f(x)在(﹣1,1)上的单调性,并给出证明.
【答案】
(1)解: f(0)=loga1=0.
因为f(x)是奇函数,
所以:f(﹣x)=﹣f(x)f(﹣x)+f(x)=0
∴loga ![]() +loga
+loga ![]() =0;
=0;
∴loga ![]() =0
=0 ![]() =1,
=1,
即∴1﹣m2x2=1﹣x2对定义域内的x都成立.∴m2=1.
所以m=1或m=﹣1(舍)
∴m=1.
(2)解:∵m=1
∴f(x)=loga ![]() ,
,
∴t= ![]() ,
,
设﹣1<x1<x2<1,则t1﹣t2= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∵﹣1<x1<x2<1∴x2﹣x1>0,(x1+1)(x2+1)>0
∴t1>t2.
当a>1时,logat1>logat2,即f(x1)>f(x2).
∴当a>1时,f(x)在(﹣1,1)上是减函数.
当0<a<1时,logat1<logat2,即f(x1)<f(x2).
∴当0<a<1时,f(x)在(﹣1,1)上是增函数
【解析】(1)f(0)=loga1=0,利用奇函数的定义,即可求出实数m的值;(2)当m=1时,f(x)=loga ![]() ,t=
,t= ![]() ,判断其单调性,即可判断与证明函数f(x)在(﹣1,1)上的单调性
,判断其单调性,即可判断与证明函数f(x)在(﹣1,1)上的单调性
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较,以及对函数奇偶性的性质的理解,了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
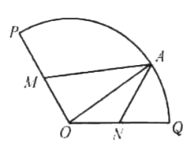
【题目】某校有一块圆心![]() ,半径为200米,圆心角为
,半径为200米,圆心角为![]() 的扇形绿地
的扇形绿地![]() ,半径
,半径![]() 的中点分别为
的中点分别为![]() ,
,![]() 为弧
为弧![]() 上的一点,设
上的一点,设![]() ,如图所示,拟准备两套方案对该绿地再利用.
,如图所示,拟准备两套方案对该绿地再利用.
(1)方案一:将四边形绿地![]() 建成观赏鱼池,其面积记为
建成观赏鱼池,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式,并求
的函数关系式,并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
(2)方案二:将弧![]() 和线段
和线段![]() 围成区域建成活动场地,其面积记为
围成区域建成活动场地,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式;并求
的函数关系式;并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为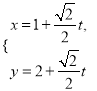 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与圆
与圆![]() 相交于不同的
相交于不同的![]() ,
, ![]() 两点.
两点.
(1)求线段![]() 垂直平分线
垂直平分线![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,求过点
,求过点![]() 与圆
与圆![]() 相切的切线方程.
相切的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 分别为等差数列和等比数列,
分别为等差数列和等比数列, ![]() ,
, ![]() 的前
的前![]() 项和为
项和为![]() .函数
.函数![]() 的导函数是
的导函数是![]() ,有
,有![]() ,且
,且![]() 是函数
是函数![]() 的零点.
的零点.
(1)求![]() 的值;
的值;
(2)若数列![]() 公差为
公差为![]() ,且点
,且点![]() ,当
,当![]() 时所有点都在指数函数
时所有点都在指数函数![]() 的图象上.
的图象上.
请你求出![]() 解析式,并证明:
解析式,并证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:

测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
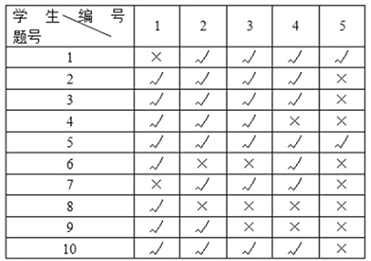
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;

(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com