
【题目】如图,在三棱柱ABC![]() 中,侧面
中,侧面![]() 是矩形,∠BAC=90°,
是矩形,∠BAC=90°,![]() ⊥BC,
⊥BC,![]() =AC=2AB=4,且
=AC=2AB=4,且![]() ⊥
⊥![]() .
.

(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)设D是![]() 的中点,判断并证明在线段
的中点,判断并证明在线段![]() 上是否存在点E,使得DE∥平面
上是否存在点E,使得DE∥平面![]() .若存在,求二面角E
.若存在,求二面角E![]() B的余弦值.
B的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)易知![]() ⊥平面ABC,有
⊥平面ABC,有![]() ⊥AC,依次可证得
⊥AC,依次可证得![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,从而得证;
,从而得证;
(2)当E为![]() 的中点时,连接AE,
的中点时,连接AE,![]() ,DE,易证得平面EFD∥平面
,DE,易证得平面EFD∥平面![]() ,以 A为坐标原点,AB,AC,
,以 A为坐标原点,AB,AC,![]() 所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,分别求面
所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,分别求面![]() 和面
和面![]() 的法向量,由法向量的夹角可求二面角的余弦值.
的法向量,由法向量的夹角可求二面角的余弦值.
详解:(1)在三棱柱ABC![]() 中,侧面
中,侧面![]() 是矩形,∴
是矩形,∴![]() ⊥AB,
⊥AB,
又![]() ⊥BC,AB∩BC=B,
⊥BC,AB∩BC=B,
∴![]() ⊥平面ABC,∴
⊥平面ABC,∴![]() ⊥AC.
⊥AC.
又![]() =AC,∴
=AC,∴![]() ⊥
⊥![]() .
.
又![]() ⊥
⊥![]() ,
,![]() ∩
∩![]() =
=![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,
,
又![]()
![]() 平面
平面![]() ,∴平面
,∴平面![]() ⊥平面
⊥平面![]() .
.
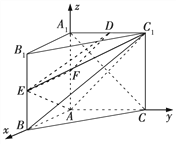
图1
(2)解法一 当E为![]() 的中点时,连接AE,
的中点时,连接AE,![]() ,DE,如图1,取
,DE,如图1,取![]() 的中点F,连接EF,FD,
的中点F,连接EF,FD,
∵EF∥AB,DF∥![]() ,
,
又EF∩DF=F,AB∩![]() =A,
=A,
∴平面EFD∥平面![]() ,
,
则有DE∥平面![]() .
.
以 A为坐标原点,AB,AC,![]() 所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,因为
所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,因为![]() =AC=2AB=4,
=AC=2AB=4,
∴A(0,0,0),B(2,0,0),![]() (0,4,4),C(0,4,0),E(2,0,2),
(0,4,4),C(0,4,0),E(2,0,2),![]() (0,0,4),由(1)知,
(0,0,4),由(1)知,![]() =(0,4,4)是平面
=(0,4,4)是平面![]() 的一个法向量.
的一个法向量.
设n=(x,y,z)为平面![]() 的法向量,
的法向量,
∵![]() =(0,4,4),
=(0,4,4),![]() =(2,0,2),
=(2,0,2),
∴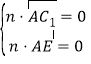
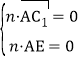 ,即
,即![]()
![]() ,
,
令z=1,则x=1,y=1,
∴n=(1,1,1)为平面![]() 的一个法向量.
的一个法向量.
设![]()
![]() 与n的夹角为θ,则cos θ=
与n的夹角为θ,则cos θ=![]() =
=![]()
![]() ,由图知二面角E
,由图知二面角E![]() B为锐角,∴二面角E
B为锐角,∴二面角E![]() B的余弦值为
B的余弦值为![]()
![]() .
.
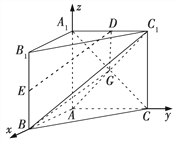
图2
解法二 当E为![]() 的中点时,连接DE,如图2,设
的中点时,连接DE,如图2,设![]() 交
交![]() 于点G,连接BG,DG,∵BE
于点G,连接BG,DG,∵BE![]() DG,∴四边形DEBG为平行四边形,
DG,∴四边形DEBG为平行四边形,
则DE∥BG,又DE![]() 平面
平面![]() ,BG
,BG![]() 平面
平面![]() ,则DE∥平面
,则DE∥平面![]() .
.
求二面角E![]() B的余弦值同解法一.
B的余弦值同解法一.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】曲一中某研究性学习小组对学习数学的练习时间与进步率的关系进行研究,他们分别记录了同班5个同学一周内的学习时间与周测成绩进步率,得到如下资料.

(1)从5个同学中任选2个,记其进步率分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)若进步率![]() 与学习时间
与学习时间![]() 服从线性关系,求出
服从线性关系,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)在这5个同学中任取3个,其中进步率超过25的有![]() 个同学,求
个同学,求![]() 的数学期望.
的数学期望.
参考公式:回归直线方程是![]() ,其中
,其中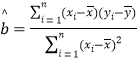
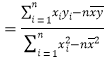
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(简称:![]() )是定量描述空气质量状况的无量纲指数,空气质量按照
)是定量描述空气质量状况的无量纲指数,空气质量按照![]() 大小分为六级:
大小分为六级:![]() 为优,
为优,![]() 为良,
为良,![]() 为轻度污染,
为轻度污染,![]() 为中度污染,
为中度污染,![]() 为重度污染,
为重度污染,![]() 为严重污染.下面记录了北京市
为严重污染.下面记录了北京市![]() 天的空气质量指数,根据图表,下列结论错误的是( )
天的空气质量指数,根据图表,下列结论错误的是( )

A. 在北京这![]() 天的空气质量中,按平均数来考察,最后
天的空气质量中,按平均数来考察,最后![]() 天的空气质量优于最前面
天的空气质量优于最前面![]() 天的空气质量 B. 在北京这
天的空气质量 B. 在北京这![]() 天的空气质量中,有
天的空气质量中,有![]() 天达到污染程度
天达到污染程度
C. 在北京这![]() 天的空气质量中,12月29日空气质量最好 D. 在北京这
天的空气质量中,12月29日空气质量最好 D. 在北京这![]() 天的空气质量中,达到空气质量优的天数有
天的空气质量中,达到空气质量优的天数有![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,BC=3,AB=4,AC=CC1=5,M,N分别是A1B,B1C1的中点.
(1)求证:MN//平面ACC1A1;
(2)求点N到平面MBC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解中学生课余观看热门综艺节目“爸爸去哪儿”是否与性别有关,某中学一研究性学习小组从该校学生中随机抽取了![]() 人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的
人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的![]() ,男生喜欢看该节目的占男生总人数的
,男生喜欢看该节目的占男生总人数的![]() .随后,该小组采用分层抽样的方法从这
.随后,该小组采用分层抽样的方法从这![]() 份问卷中继续抽取了
份问卷中继续抽取了![]() 份进行重点分析,知道其中喜欢看该节目的有
份进行重点分析,知道其中喜欢看该节目的有![]() 人.
人.
(1) 现从重点分析的![]() 人中随机抽取了
人中随机抽取了![]() 人进行现场调查,求这两人都喜欢看该节目的概率;
人进行现场调查,求这两人都喜欢看该节目的概率;
(2) 若有![]() 的把握认为“爱看该节目与性别有关”,则参与调查的总人数
的把握认为“爱看该节目与性别有关”,则参与调查的总人数![]() 至少为多少?
至少为多少?
参考数据:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是函数
是函数![]() 的图像上任意不同的两点,依据图像可知,线段
的图像上任意不同的两点,依据图像可知,线段![]() 总是位于
总是位于![]() 两点之间函数图像的上方,因此有结论
两点之间函数图像的上方,因此有结论![]() 成立,运用类比的思想方法可知,若点
成立,运用类比的思想方法可知,若点![]() ,
,![]() 是函数
是函数![]() 的图像上任意不同的两点,则类似地有_________成立.
的图像上任意不同的两点,则类似地有_________成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.

求:(1)高一参赛学生的成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com