练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数

    （1）求函数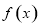的最大值；

    （2）若的取值范围.

     

    （1）0；（2）

    【解析】

    试题分析：（1）先求，再利用判断函数的单调性并求最值；

    （2）由题设知先求其导数得

    因为，所以，可分，，三种情况探究，进而得到函数变化性质，并从中找出满足的的取值范围.

    【解析】
    （1）， 1分

    当时，；当时，；当时，；

    所以函数在区间上单调递增，在区间上单调递减； 3分

    故. 4分

    （2）由，得． 6分

    当时，由（1）得成立； 8分

    当时，因为时，所以时，

    成立； 10分

    当时，因为时，所以． 13分

    综上，知的取值范围是. 14分

    考点：1、导数在研究函数性质中的应用；2、分类讨论的思想.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年山东省烟台市高三5月适应性训练一文科数学试卷（解析版） 题型：解答题

    在数列中，已知,,.

    （1）求数列的通项公式；

    （2）设数列，求的前项和.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省潍坊市高三4月模拟考试文科数学试卷（解析版） 题型：选择题

    已知双曲线 的左、右焦点分别是、过垂直x轴的直线与双曲线C的两渐近线的交点分别是M、N，若为正三角形，则该双曲线的离心率为（ ）

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷（解析版） 题型：填空题

    已知等比数列________.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷（解析版） 题型：选择题

    设是两个非零向量，则下列命题为真命题的是

    A.若

    B.若

    C.若，则存在实数，使得

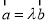    D.若存在实数，使得，则

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省淄博市高三复习阶段性诊断考试文科数学试卷（解析版） 题型：解答题

    在中，角A,B,C的对边分别为a,b,c，若.

    （1）求B；

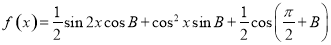    （2）设函数，求函数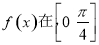上的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省淄博市高三复习阶段性诊断考试文科数学试卷（解析版） 题型：选择题

    函数的部分图象如图所示，则的解析式可以是

    A. B.

    C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省济南市高三3月考模拟考试理科数学试卷（解析版） 题型：填空题

    航天员拟在太空授课，准备进行标号为0，1，2，3，4，5的六项实验，向全世界人民普及太空知识，其中0号实验不能放在第一项，最后一项的标号小于它前面相邻一项的标号，则实验顺序的编排方法种数为 (用数字作答)．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省日照市高三5月统一质量检测考试理科数学试卷（解析版） 题型：填空题

    在平面几何中有如下结论：若正三角形ABC的内切圆面积为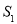，外接圆面积为，则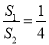.推广到空间几何体中可以得到类似结论：若正四面体ABCD的内切球体积为，外接球体积为，则=___________.

     

    查看答案和解析>>

    同步练习册答案