Question

18．函数f（x）=$\left\{\begin{array}{l}{2^x}-\frac{1}{x}-1\;，\;x＜0\;\\ lnx-{x^2}+2x\;，\;x＞0\end{array}$的零点的个数为3．

Answer 1

分析 函数f（x）=$\left\{\begin{array}{l}{2^x}-\frac{1}{x}-1\;，\;x＜0\;\\ lnx-{x^2}+2x\;，\;x＞0\end{array}$的零点的个数转化为方程${2}^{x}-1=\frac{1}{x}..（x＜0）$ 及lnx=x²-2x..（x＞0）的根的个数，结合图象即可．

解答 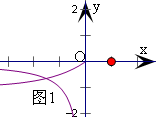解：函数f（x）=$\left\{\begin{array}{l}{2^x}-\frac{1}{x}-1\;，\;x＜0\;\\ lnx-{x^2}+2x\;，\;x＞0\end{array}$的零点的个数
转化为方程${2}^{x}-1=\frac{1}{x}..（x＜0）$ 及lnx=x²-2x..（x＞0）的根的个数，
结合图象1，方程${2}^{x}-1=\frac{1}{x}..（x＜0）$ 有一个根，
结合图象2，方程lnx=x²-2x..（x＞0）有2个根，
故一共有3个根，即3个零点．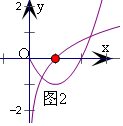
故答案为：3

点评 本题考查了分段函数零点问题，转化思想是关键，属于基础题．