练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    给出下列四个命题：

    ①命题“若α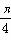＝，则tan α＝1”的逆否命题为假命题；

    ②命题p：∀x∈R，sin x≤1.则綈p：∃x0∈R，使sin x0>1；

    ③“φ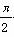＝＋kπ(k∈Z)”是“函数y＝sin(2x＋φ)为偶函数”的充要条件；

    ④命题p：“∃x0∈R，使sin x0＋cos x0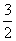＝”；命题q：“若sin α>sin β，则α>β ”，那么(綈p)∧q为真命题．

    其中正确的个数是(　　)

    A．1  B．2  C．3  D．4


    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知双曲线与椭圆有共同的焦点，点在双曲线上.

    （I）求双曲线的方程；

    （II）以为中点作双曲线的一条弦，求弦所在直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c三个实数中，有且只有一个是负数，设计一个程序，筛选出这个负数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列说法中正确的是(　　)

    A．“x>5”是“x>3”必要不充分条件

    B．命题“对∀x∈R，恒有x2＋1>0”的否定是“∃x∈R，使得x2＋1≤0”

    C．∃m∈R，使函数f(x)＝x2＋mx(x∈R)是奇函数

    D．设p，q是简单命题，若p∨q是真命题，则p∧q也是真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    命题p：∀x∈R,2x>1，则綈p：________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若集合A＝{0,1,2，x}，B＝{1，x2}，A∪B＝A，则满足条件的实数x有(　　)

    A．1个  B．2个  C．3个  D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{x|x2－2x－3≤0}，B＝{x|m－2≤x≤m＋2，m∈R}．

    (1)若A∪B＝A，求实数m的取值；

    (2)若A∩B＝{x|0≤x≤3}，求实数m的值；

    (3)若A⊆∁RB，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     (1)具有性质：f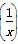＝－f(x)的函数，我们称为满足“倒负”交换的函数，下列函数：

    ①f(x)＝x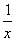－；②f(x)＝x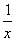＋；③f(x)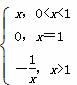＝中满足“倒负”变换的函数是(　　)

    A．①②  B．①③  C．②③  D．只有①

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若二次函数f(x)＝ax2＋bx＋c(a≠0)满足f(x＋1)－f(x)＝2x，且f(0)＝1.

    (1)求f(x)的解析式；

    (2)若在区间[－1,1]上，不等式f(x)>2x＋m恒成立，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案