
 由四个全等的等边三角形的封面几何体称为正四面体,如图,正四面体ABCD中,E、F分别是棱BC、AD的中点,CF与DE是一对异面直线,在图形中适当的选取一点作出异面直线CF、DE的平行线,找出异面直线CF与DE成的角.(注:至少用四种方法)
由四个全等的等边三角形的封面几何体称为正四面体,如图,正四面体ABCD中,E、F分别是棱BC、AD的中点,CF与DE是一对异面直线,在图形中适当的选取一点作出异面直线CF、DE的平行线,找出异面直线CF与DE成的角.(注:至少用四种方法) 分析 【方法一】如图1所示,找出∠CFG是异面直线CF与DE所成的角(或其补角),用余弦定理求即可;
【方法二】如图2所示,找出∠FCM是异面直线CF与DE所成的角(或其补角);用余弦定理求出即可;
【方法三】如图3所示,找出∠NED是异面直线CF与DE所成的角(或其补角),利用余弦定理求出即可;
【方法四】如图4所示,利用向量法,以{$\overrightarrow{CA}$,$\overrightarrow{CB}$,$\overrightarrow{CD}$}为基底,表示出$\overrightarrow{DE}$与$\overrightarrow{CF}$,求出两向量所成的角,即可求出异面直线AE与CF所成的角.
解答 解:【方法一】如图1所示,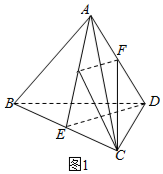
过点F作FG∥DE,交AE与点G,连接GC,则∠CFG是异面直线CF与DE所成的角(或其补角);
设AB=1,则DE=CF=AE=$\frac{\sqrt{3}}{2}$,GF=$\frac{1}{2}$DE=$\frac{\sqrt{3}}{4}$;
GC=$\sqrt{{GE}^{2}{+EC}^{2}}$=$\sqrt{{(\frac{\sqrt{3}}{4})}^{2}{+(\frac{1}{2})}^{2}}$=$\sqrt{\frac{7}{16}}$,
cos∠CFG=$\frac{{GF}^{2}{+CF}^{2}{-GC}^{2}}{2GF•CF}$=$\frac{\frac{3}{16}+\frac{3}{4}-\frac{7}{16}}{2×\frac{\sqrt{3}}{4}×\frac{\sqrt{3}}{2}}$=$\frac{2}{3}$,
∴∠CFG=arccos$\frac{2}{3}$.
【方法二】如图2所示,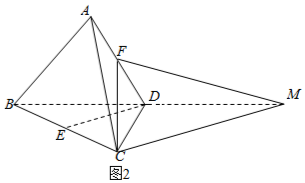
过点C作CM∥ED,交BD的延长线与点M,连接FM,则∠FCM是异面直线CF与DE所成的角(或其补角);
设AB=1,则DE=CF=$\frac{\sqrt{3}}{2}$,∴CM=2DE=$\sqrt{3}$,
FM2=DF2+DM2-2DF•DM•cos120°=${(\frac{1}{2})}^{2}$+12-2×$\frac{1}{2}$×1×(-$\frac{1}{2}$)=$\frac{7}{4}$,
∴cos∠FCM=$\frac{{FC}^{2}{+CM}^{2}{-FM}^{2}}{2FC•CM}$=$\frac{\frac{3}{4}+3-\frac{7}{4}}{2×\frac{\sqrt{3}}{2}×\sqrt{3}}$=$\frac{2}{3}$,
∴∠FCM=arccos$\frac{2}{3}$;
【方法三】如图3所示,连接BF,取BF的中点N,连接EN,DN,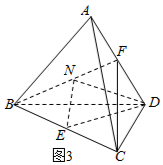
则EN∥FC,且EN=$\frac{1}{2}$FC,∴∠NED是异面直线CF与DE所成的角(或其补角),利用余弦定理求出即可;
【方法四】如图4所示,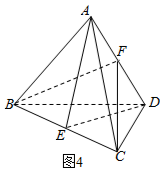
向量法,$\overrightarrow{CF}$=$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CD}$),$\overrightarrow{DE}$=$\overrightarrow{CE}$-$\overrightarrow{CD}$=$\frac{1}{2}$$\overrightarrow{CB}$-$\overrightarrow{CD}$;
设正四面体的棱长为1,则|$\overrightarrow{CF}$|=|$\overrightarrow{DE}$|=$\frac{\sqrt{3}}{2}$,
∴$\overrightarrow{CF}$•$\overrightarrow{DE}$=$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CD}$)•($\frac{1}{2}$$\overrightarrow{CB}$-$\overrightarrow{CD}$)
=$\frac{1}{4}$$\overrightarrow{CA}$•$\overrightarrow{CB}$-$\frac{1}{2}$$\overrightarrow{CA}$•$\overrightarrow{CD}$+$\frac{1}{4}$$\overrightarrow{CD}$•$\overrightarrow{CB}$-$\frac{1}{2}$${\overrightarrow{CD}}^{2}$
=$\frac{1}{8}$-$\frac{1}{4}$+$\frac{1}{8}$-$\frac{1}{2}$=-$\frac{1}{2}$;
∴cos<$\overrightarrow{CF}$,$\overrightarrow{DE}$>=$\frac{\overrightarrow{CF}•\overrightarrow{DE}}{|\overrightarrow{CF}|×|\overrightarrow{DE}|}$=$\frac{-\frac{1}{2}}{\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}}$=-$\frac{2}{3}$,
∴异面直线AE与CF所成角的余弦值为$\frac{2}{3}$,
AE与CF所成角为arccos$\frac{2}{3}$.
点评 本题考查了异面直线所成的角的计算问题,解题时找角是关键,也可以用向量的方法求解,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}π$ | B. | $\frac{π}{2}$ | C. | $\frac{\sqrt{3}}{2}π$ | D. | $\frac{\sqrt{3}}{4}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
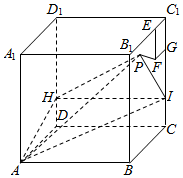 如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )
如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )| A. | $\frac{2\sqrt{17}}{3}$ | B. | $\frac{25}{6}$ | C. | $\frac{2\sqrt{17}}{3}$(10-3$\sqrt{2}$) | D. | $\frac{20}{3}$-2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com