
分析 构造辅助函数g(x)=f(x)-$\frac{1}{4}{x}^{4}$,由题意可得g(x)是偶函数,求导判断g(x)的单调性,把f(m-3)-f(m)≥$\frac{1}{4}$[(m-3)4-m4]转化为g(m-3)≥g(m),利用单调性转化为关于m的不等式求解.
解答 解:令g(x)=f(x)-$\frac{1}{4}{x}^{4}$,
∵g(-x)-g(x)=f(-x)-$\frac{1}{4}(-x)^{4}$-f(x)-$\frac{1}{4}{x}^{4}$=0,
∴函数g(x)为偶函数,
∵x∈[0,+∞)时,g′(x)=f′(x)-x3<0,
∴函数g(x)在x∈[0,+∞)为减函数,
f(m-3)-f(m)≥$\frac{1}{4}$[(m-3)4-m4],即f(m-3)-$\frac{1}{4}(m-3)^{4}$≥f(m)-$\frac{1}{4}{m}^{4}$,
也即g(m-3)≥g(m),
∴g(|m-3|)≥g(|m|),
则|m-3|≤|m|,解得:m$≥\frac{3}{2}$.
∴实数m的取值范围为[$\frac{3}{2}$,+∞).
故答案为:[$\frac{3}{2}$,+∞).
点评 本题考查利用导数研究函数的单调性,考查数学转化思想方法,正确构造函数是关键,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 如果a∥α,b∥α,那么a∥b | |
| B. | 如果a∥b,a∥α,b?α,那么b∥α | |
| C. | 如果a∥b,那么α平行于经过b的任何平面 | |
| D. | 如果a∥α,那么a与α内的任何直线平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
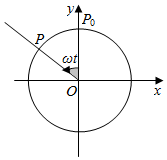 如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).
如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com