
| 2x-1 |
| x+1 |
| 2x-1 |
| x+1 |
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
| 3 |
| x1+1 |
| 3 |
| x2+1 |
| 3 |
| x2+1 |
| 3 |
| x1+1 |
| 3(x1-x2) |
| (x1+1)(x2+1) |
| 2×5-1 |
| 5+1 |
| 3 |
| 2 |
| 2×3-1 |
| 3+1 |
| 5 |
| 4 |


科目:高中数学 来源: 题型:
| A、6*SQR(4)+3^2*2=154 |
| B、3*(5+4)+SQR(9)^2=17 |
| C、[5+3*(12-7)]/4=5 |
| D、(2+3)*5-4+2*3*SQR(4)^2=72 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,函数y=
如图,函数y=| x | ||
|
| ||
| x |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| x | ||
|
| ||
| x |
| A、1个 | B、2个 | C、3个 | D、4个. |
查看答案和解析>>
科目:高中数学 来源: 题型:
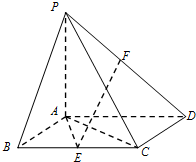 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.查看答案和解析>>
科目:高中数学 来源: 题型:
 某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如表):
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如表):| 网购金额 (单位:千元) |
频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com