
【题目】已知空间9点集![]() ,其中任意四点不共面.在这9个点间联结若干条线段,构成一个图G,使图中不存在四面体.问图G中最多有多少个三角形?
,其中任意四点不共面.在这9个点间联结若干条线段,构成一个图G,使图中不存在四面体.问图G中最多有多少个三角形?
【答案】27
【解析】
在一个n个点的空间图中不存在三角形,则其边数不超过![]() .
.
证明:设这n个点为![]() ,其中从
,其中从![]() 引出的边数最多,不妨设共有k条:
引出的边数最多,不妨设共有k条:![]() .依条件,不存在三角形,那么,点
.依条件,不存在三角形,那么,点![]() 之间没有边相连.从而,空间图中每条边均至少有一个端点为
之间没有边相连.从而,空间图中每条边均至少有一个端点为![]() 中的点而每个
中的点而每个![]() 至多引出k条边.因此,总边数小于或等于k
至多引出k条边.因此,总边数小于或等于k![]()
下面证明空间9点集M中,若任意4点不共面,在这9点间联结若干条线段,如果图G中已有(至少)28个三角形,则至少有一个四面体.
用反证法.
假设不存在一个四面体,在9点集![]() 中,由抽屉原理知,其中必有一点为至少
中,由抽屉原理知,其中必有一点为至少![]() 个三角形的顶点.从而,由这个点至少引出5条边,设这个点为
个三角形的顶点.从而,由这个点至少引出5条边,设这个点为![]()
(1).若从点![]() 引出5条边
引出5条边![]() ,依题意,由于没有四面体,那么,由
,依题意,由于没有四面体,那么,由![]() 这5个点构成的子图中没有三角形.由前面的结论知,这个子图中至多有
这5个点构成的子图中没有三角形.由前面的结论知,这个子图中至多有![]() 条边.从而.以
条边.从而.以![]() 为顶点的三角形至多有6个,矛盾.
为顶点的三角形至多有6个,矛盾.
(2)若从点![]() 引出6条边
引出6条边![]() ,类似(1),至多有
,类似(1),至多有![]() 个三角形以
个三角形以![]() 为顶点,矛盾.
为顶点,矛盾.
(3)若从点![]() 引出7条边
引出7条边![]() ,由于没有四面体,可知
,由于没有四面体,可知![]() 这7个点构成的子图中没有三角形,这个子图至多有
这7个点构成的子图中没有三角形,这个子图至多有![]() 条边.从而,以
条边.从而,以![]() 为顶点的三角形至多有12个,不以
为顶点的三角形至多有12个,不以![]() 为顶点的三角形必以点
为顶点的三角形必以点![]() 为一个顶点.类似地也至多有12个三角形,那么,三角形总数小于或等于12×2-24<28,矛盾.
为一个顶点.类似地也至多有12个三角形,那么,三角形总数小于或等于12×2-24<28,矛盾.
(4)若从点![]() 引出8条边
引出8条边![]() ,这时,
,这时,![]() ,A这8个点构成的子图中没有三角形.由前面的结论知,至多有
,A这8个点构成的子图中没有三角形.由前面的结论知,至多有![]() 条边.从而,原图G中至多有16个三角形,矛盾.
条边.从而,原图G中至多有16个三角形,矛盾.
于是,满足要求的三角形至多有27个.
将9点集M分成三组![]() ,
,![]() ,
,![]() ,使同组中任两点不连线,而不同组中的两点均连线,这样有
,使同组中任两点不连线,而不同组中的两点均连线,这样有![]() 个三角形,当然没有四面体.
个三角形,当然没有四面体.


科目:高中数学 来源: 题型:
【题目】2018年1月31日晚上月全食的过程分为初亏、食既、食甚、生光、复圆五个阶段,月食的初亏发生在19时48分,20时51分食既,食甚时刻为21时31分,22时08分生光,直至23时12分复圆![]() 全食伴随有蓝月亮和红月亮,全食阶段的“红月亮”将在食甚时刻开始,生光时刻结束,一市民准备在19:55至21:56之间的某个时刻欣赏月全食,则他等待“红月亮”的时间不超过30分钟的概率是
全食伴随有蓝月亮和红月亮,全食阶段的“红月亮”将在食甚时刻开始,生光时刻结束,一市民准备在19:55至21:56之间的某个时刻欣赏月全食,则他等待“红月亮”的时间不超过30分钟的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,A(x1,y1),B(x2,y2)是过F的直线与抛物线的两个交点,求证:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 为定值;
为定值;
(3)以AB为直径的圆与抛物线的准线相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为![]() (t为参数),以原点为极点,
(t为参数),以原点为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线![]() 关于
关于![]() 对称.
对称.
(1)求![]() 极坐标方程,
极坐标方程,![]() 直角坐标方程;
直角坐标方程;
(2)将![]() 向左平移4个单位长度,按照
向左平移4个单位长度,按照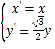 变换得到
变换得到![]() 与两坐标轴交于
与两坐标轴交于![]() 两点,
两点,![]() 为
为![]() 上任一点,求
上任一点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目,![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
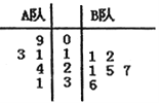
(1)根据茎叶图中的数据,求出![]() 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从![]() 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从![]() 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,平面DAC⊥底面ABC,![]() ,AD=CD=
,AD=CD=![]() ,O是AC的中点,E是BD的中点.
,O是AC的中点,E是BD的中点.
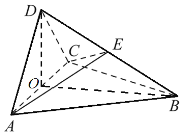
(1)证明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.在回归直线方程![]() 中,当解释变量x每增加1个单位时,预报变量
中,当解释变量x每增加1个单位时,预报变量![]() 平均增加
平均增加![]() 个单位.
个单位.
B.对分类变量X与Y,随机变量![]() 的观测值k越大,则判断“X与Y有关系”的把握程度越小.
的观测值k越大,则判断“X与Y有关系”的把握程度越小.
C.两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1.
D.回归直线过样本点的中心![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com