
分析 (1)取AB的中点D,连接OD,由中点的向量表示形式和直线和圆相交的条件,即可得到所求范围;
(2)设圆M的方程为λ(x2+y2-4)+kx-y+1=0,即为x2+y2+$\frac{k}{λ}$x-$\frac{1}{λ}$y+$\frac{1}{λ}$-4=0,求出圆心和半径,由直线和圆相切的条件,可得d=r,化简可得k2=48λ2+20λ≥0,可得λ的范围,进而得到r的最小值,即可得到圆的方程.
解答 解:(1)取AB的中点D,连接OD,
则|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=2|$\overrightarrow{OD}$|,
即为O到直线AB的距离的2倍,
由0≤|$\overrightarrow{OD}$|≤1,可得
|$\overrightarrow{OA}$+$\overrightarrow{OB}$|的范围为[0,2];
(2)设圆M的方程为λ(x2+y2-4)+kx-y+1=0,
即为x2+y2+$\frac{k}{λ}$x-$\frac{1}{λ}$y+$\frac{1}{λ}$-4=0,
圆心为(-$\frac{k}{2λ}$,$\frac{1}{2λ}$),半径r=$\sqrt{4-\frac{1}{λ}+\frac{{k}^{2}}{4{λ}^{2}}+\frac{1}{4{λ}^{2}}}$,
由圆与y=-4相切,可得|4+$\frac{1}{2λ}$|=r,
化简可得k2=48λ2+20λ,
由k2≥0,解得λ>0或λ≤-$\frac{5}{12}$,
即有λ=-$\frac{5}{12}$,r取得最小值,且为4-$\frac{6}{5}$=$\frac{14}{5}$,
此时k=0,
即有圆M的方程为x2+y2+$\frac{12}{5}$y-$\frac{32}{5}$=0.
点评 本题考查直线和圆的位置关系,考查中点的向量表示,直线和圆相切的条件以及圆的方程的求法,属于中档题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
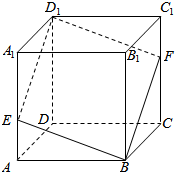 已知E,F分别是正方体A1B1C1D1-ABCD的棱AA1,CC1上的点,且A1E=2EA,CF=2FC1,求证:四边形BED1F是平行四边形.
已知E,F分别是正方体A1B1C1D1-ABCD的棱AA1,CC1上的点,且A1E=2EA,CF=2FC1,求证:四边形BED1F是平行四边形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com