
已知函数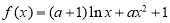 .
.
(1)讨论函数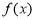 的单调性;
的单调性;
(2)设 ,证明:对任意
,证明:对任意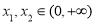 ,
, .
.
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)先求导数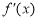 ,利用导数求函数
,利用导数求函数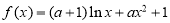 的单调区间,注意要对参变量
的单调区间,注意要对参变量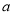 的取值进行分类讨论;
的取值进行分类讨论;
(2)由(1)的结论知当a≤-2时, f(x)在(0,+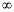 )单调递减;设x1≥x2.
)单调递减;设x1≥x2.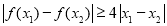 等价于
等价于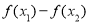 ≥4x1-4x2,进一步转化为函数g(x)=f(x)+4x在(0,+
≥4x1-4x2,进一步转化为函数g(x)=f(x)+4x在(0,+ )的单调性问题解决.
)的单调性问题解决.
试题解析:【解析】
(1) f(x)的定义域为(0,+ ),
),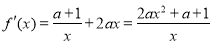 . 1分
. 1分
当a≥0时,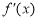 >0,故f(x)在(0,+
>0,故f(x)在(0,+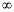 )单调递增; 3分
)单调递增; 3分
当a≤-1时,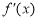 <0, 故f(x)在(0,+
<0, 故f(x)在(0,+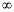 )单调递减; 5分
)单调递减; 5分
当-1<a<0时,令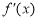 =0,解得x=
=0,解得x=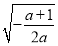 .当x∈(0,
.当x∈(0,  )时,
)时,  >0;
>0;
x∈( ,+
,+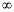 )时,
)时,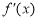 <0, 故f(x)在(0,
<0, 故f(x)在(0, 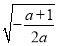 )单调递增,在(
)单调递增,在(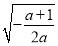 ,+
,+ )单调递减. 7分
)单调递减. 7分
(2)不妨假设x1≥x2.由于a≤-2,故f(x)在(0,+ )单调递减. 8分
)单调递减. 8分
所以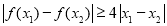 等价于
等价于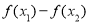 ≥4x1-4x2,
≥4x1-4x2,
即f(x2)+ 4x2≥f(x1)+ 4x1. 10分
令g(x)=f(x)+4x,则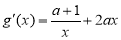 +4=
+4=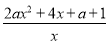
于是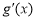 ≤
≤ =
=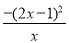 ≤0. 12分
≤0. 12分
从而g(x)在(0,+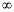 )单调递减,故g(x1) ≤g(x2),
)单调递减,故g(x1) ≤g(x2),
即 f(x1)+ 4x1≤f(x2)+ 4x2,故对任意x1,x2∈(0,+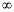 ) ,
) ,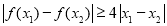 . 14分
. 14分
考点:导数在研究函数性质中的应用


科目:高中数学 来源:2015届广东省惠州市高三第二次调研考试理科数学试卷(解析版) 题型:选择题
某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数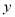 与该班人数
与该班人数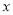 之间的函数关系用取整函数
之间的函数关系用取整函数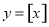 (
(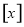 表示不大于
表示不大于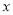 的最大整数)可以表示为( )
的最大整数)可以表示为( )
A.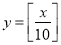 B.
B.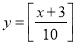 C.
C.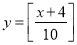 D.
D.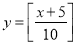
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测理科数学试卷(解析版) 题型:选择题
若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示,
则此几何体的体积等于( )
A. B.
B. C.
C. D.
D.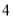
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:选择题
给出四个函数,分别满足①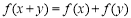 ;②
;②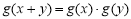 ;③
;③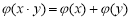 ;④
;④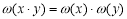 ,又给出四个函数的图象如下:
,又给出四个函数的图象如下:

则正确的配匹方案是( )
A.①—M ②—N ③—P ④—Q
B.①—N ②—P ③—M ④—Q
C.①—P ②—M ③—N ④—Q
D.①—Q ②—M ③—N ④—P
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:填空题
某班收集了50位同学的身高数据,每一个学生的性别与其身高是否高于或低于中位数的列联表如下:
| 高于中位数 | 低于中位数 | 总计 |
男 | 20 | 7 | 27 |
女 | 10 | 13 | 23 |
总计 | 30 | 20 | 50 |
为了检验性别是否与身高有关系,根据表中的数据,得到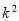 的观测值
的观测值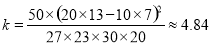 ,
,
因为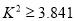 ,所以在犯错误的概率不超过 _________ 的前提下认为性别与身高有关系.
,所以在犯错误的概率不超过 _________ 的前提下认为性别与身高有关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com