
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的一个短轴端点及两个焦点构成的三角形的面积为
,以椭圆的一个短轴端点及两个焦点构成的三角形的面积为![]() ,圆C方程为
,圆C方程为![]() .
.
(1)求椭圆及圆C的方程;
(2)过原点O作直线l与圆C交于A,B两点,若![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)椭圆的方程![]() ,圆的方程为
,圆的方程为![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)由离心率为![]() 可得
可得![]() ,结合
,结合![]() 得
得![]() ,根据以椭圆的一个短轴端点及两个焦点为顶点的三角形面积为
,根据以椭圆的一个短轴端点及两个焦点为顶点的三角形面积为![]() 可得
可得![]() ,从而求的
,从而求的![]() ,得到椭圆和圆的方程;(2)设出直线
,得到椭圆和圆的方程;(2)设出直线![]() 的方程,整理方程组,由判别式求出直线斜率的范围,韦达定理得到
的方程,整理方程组,由判别式求出直线斜率的范围,韦达定理得到![]() 坐标的关系,根据向量数量积的坐标表示列出方程,求的斜率
坐标的关系,根据向量数量积的坐标表示列出方程,求的斜率![]() .
.
试题解析:(1)设椭圆的焦距为2c,左、右焦点分别为![]() ,由椭圆的离心率为
,由椭圆的离心率为![]() 可得
可得![]() ,即
,即![]() ,所以
,所以![]()
以椭圆的一个短轴端点及两个焦点为顶点的三角形的面积为![]() ,即
,即![]() ,
,![]()
所以椭圆的方程![]() ,圆的方程为
,圆的方程为![]()
(2)①当直线![]() 的斜率不存时,直线方程为
的斜率不存时,直线方程为![]() ,与圆C相切,不符合题意
,与圆C相切,不符合题意
②当直线![]() 的斜率存在时,设直线方程
的斜率存在时,设直线方程![]() ,
,
由![]() 可得
可得![]() ,
,
由条件可得![]() ,即
,即![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
![]()
而圆心C的坐标为(2,1)则![]()
![]() ,
,
所以![]() ,
,
即![]()
所以![]() 解得
解得![]() 或
或![]()
![]() 或
或![]()


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
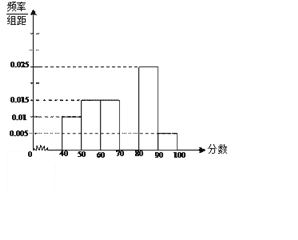
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ) 求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 设学生甲、乙的成绩属于区间[40,50),现从成绩属于该区间的学生中任选两人,求甲、乙中至少有一人被选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】刘老师是一位经验丰富的高三理科班班主任,经长期研究,他发现高中理科班的学生的数学成绩(总分150分)与理综成绩(物理、化学与生物的综合,总分300分)具有较强的线性相关性,以下是刘老师随机选取的八名学生在高考中的数学得分x与理综得分y(如下表):
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数x | 52 | 64 | 87 | 96 | 105 | 123 | 132 | 141 |
理综分数y | 112 | 132 | 177 | 190 | 218 | 239 | 257 | 275 |
参考数据及公式: ![]() .
.
(1)求出y关于x的线性回归方程;
(2)若小汪高考数学110分,请你预测他理综得分约为多少分?(精确到整数位);
(3)小金同学的文科一般,语文与英语一起能稳定在215分左右.如果他的目标是在
高考总分冲击600分,请你帮他估算他的数学与理综大约分别至少需要拿到多少分?(精确到整数位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年天猫五一活动结束后,某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得概率分布直方图如图所示:记年龄在![]() ,
, ![]() ,
, ![]() 对应的小矩形的面积分别是
对应的小矩形的面积分别是![]() ,且
,且![]() .
.
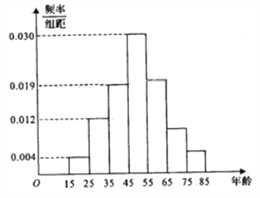
(1)以频率作为概率,若该地区五一消费超过3000元的有30000人,试估计该地区在五一活动中消费超过3000元且年龄在![]() 的人数;
的人数;
(2)若按照分层抽样,从年龄在![]() 的人群中共抽取6人,再从这6人中随机抽取2人作深入调查,求至少有1人的年龄在
的人群中共抽取6人,再从这6人中随机抽取2人作深入调查,求至少有1人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 满足:对任意
满足:对任意![]() ,
,![]() ,都有
,都有![]() 成立,且
成立,且![]() 时,
时,![]() .
.
(1)求![]() 的值,并证明:当
的值,并证明:当![]() 时,
时,![]() ;
;
(2)判断![]() 的单调性并加以证明;
的单调性并加以证明;
(3)若函数![]() 在
在![]() 上递减,求实数
上递减,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合计 | 40 | 120 | 160 |
下面临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的分别列和期望;
的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点,问:是否存在直线
两点,问:是否存在直线![]() ,使以
,使以![]() 为直径的圆经过原点
为直径的圆经过原点![]() ,若存在,求出对应直线
,若存在,求出对应直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com