
ЁОЬтФПЁПКтжнЪаСйдцжабЇИпЖўФГаЁзщЫцЛњЕїВщмНШиЩчЧј160ИіШЫЃЌвдбаОПетвЛЩчЧјОгУёдк20ЃК00-22:00ЪБМфЖЮЕФанЯаЗНЪНгыадБ№ЕФЙиЯЕЃЌЕУЕНЯТУцЕФЪ§ОнБэЃК
анЯаЗНЪН адБ№ | ПДЕчЪг | ПДЪщ | КЯМЦ |
Фа | 20 | 100 | 120 |
ХЎ | 20 | 20 | 40 |
КЯМЦ | 40 | 120 | 160 |
ЯТУцСйНчжЕБэЃК
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
ЃЈЂёЃЉНЋДЫбљБОЕФЦЕТЪЙРМЦЮЊзмЬхЕФИХТЪЃЌЫцЛњЕїВщ3УћдкИУЩчЧјЕФФаадЃЌЩшЕїВщЕФ3ШЫдкетвЛЪБМфЖЮвдПДЪщЮЊанЯаЗНЪНЕФШЫЪ§ЮЊЫцЛњБфСП![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжБ№СаКЭЦкЭћЃЛ
ЕФЗжБ№СаКЭЦкЭћЃЛ
ЃЈЂђЃЉИљОнвдЩЯЪ§ОнЃЌФмЗёга99%ЕФАбЮеШЯЮЊЁАдк20:00-22:00ЪБМфЖЮЕФанЯаЗНЪНгыадБ№гаЙиЯЕЁБЃП
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЈЂђЃЉга99%ЕФАбЮе
ЃЈЂђЃЉга99%ЕФАбЮе
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈIЃЉЯШИљОнЪ§ОнБэЧѓЕУУПИіФаЩњдкетвЛЪБМфЖЮвдПДЪщЮЊанЯаЗНЪНЕФИХТЪЃЌШЛКѓРћгУЖўЯюЗжВМаДГіЗжВМСаВЂЧѓГіЪ§бЇЦкЭћ.ЃЈ2ЃЉЭЈЙ§МЦЫу![]() ЃЌЙЪга
ЃЌЙЪга![]() АбЮе.
АбЮе.
ЪдЬтНтЮіЃКЃЈIЃЉвРЬтвтЃЌЫцЛњБфСП![]() ЕФШЁжЕЮЊ0,1,2,3ЃЌЧвУПИіФаЩњдкетвЛЪБМфЖЮвдПДЪщЮЊанЯаЗНЪНЕФИХТЪЮЊ
ЕФШЁжЕЮЊ0,1,2,3ЃЌЧвУПИіФаЩњдкетвЛЪБМфЖЮвдПДЪщЮЊанЯаЗНЪНЕФИХТЪЮЊ![]() ,
,
![]() ,
,![]()
![]() ,
,![]()
Ыљвд![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 0 | 1 | 2 | 3 |
|
|
|
|
|
Ыљвд![]() .
.
ЃЈЂђЃЉИљОнбљБОЬсЙЉЕФ![]() СаСЊБэПЩЕУ
СаСЊБэПЩЕУ
![]()
ЫљвдЮвУЧга99%ЕФАбЮеШЯЮЊЁАдк20:00-22:00ЪБМфЖЮадБ№гыанЯаЗНЪНгаЙиЁБ.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧЬнаЮPBCDжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌAЮЊPDЕФжаЕуЃЌШчЭМЃЎНЋЁїPABбиABелЕНЁїSABЕФЮЛжУЃЌЪЙSBЁЭBCЃЌЕуEдкSDЩЯЃЌЧв
ЃЌAЮЊPDЕФжаЕуЃЌШчЭМЃЎНЋЁїPABбиABелЕНЁїSABЕФЮЛжУЃЌЪЙSBЁЭBCЃЌЕуEдкSDЩЯЃЌЧв![]() ЃЌШчЭМЃЎ
ЃЌШчЭМЃЎ
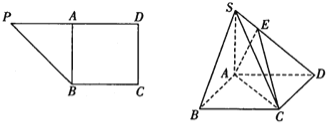
ЃЈЂёЃЉЧѓжЄЃКSAЁЭЦНУцABCDЃЛ
ЃЈЂђЃЉЧѓЖўУцНЧEЉACЉDЕФе§ЧажЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌвдЭждВЕФвЛИіЖЬжсЖЫЕуМАСНИіНЙЕуЙЙГЩЕФШ§НЧаЮЕФУцЛ§ЮЊ
ЃЌвдЭждВЕФвЛИіЖЬжсЖЫЕуМАСНИіНЙЕуЙЙГЩЕФШ§НЧаЮЕФУцЛ§ЮЊ![]() ЃЌдВCЗНГЬЮЊ
ЃЌдВCЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВМАдВCЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§дЕуOзїжБЯпlгыдВCНЛгкAЃЌBСНЕуЃЌШє![]() ЃЌЧѓжБЯпlЕФЗНГЬ.
ЃЌЧѓжБЯпlЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§f(x)ЃНexЃaxЃ2.
ЃЈ1ЃЉЧѓf(x)ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШєaЃН1ЃЌkЮЊећЪ§ЃЌЧвЕБx>0ЪБЃЌ(xЃk)fЁф(x)ЃЋxЃЋ1>0ЃЌЧѓkЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌ
ЃЌ
Цфжа![]() ЃЌШєКЏЪ§
ЃЌШєКЏЪ§![]() ЃЌЧвЫќЕФзюаЁе§жмЦкЮЊ
ЃЌЧвЫќЕФзюаЁе§жмЦкЮЊ![]() ЃЎ
ЃЎ
ЃЈЦеЭЈжабЇжЛзі1ЃЌ2ЮЪЃЉ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЌВЂЧѓГіКЏЪ§
ЕФжЕЃЌВЂЧѓГіКЏЪ§![]() ЕФЕЅЕїЕндіЧјМфЃЛ
ЕФЕЅЕїЕндіЧјМфЃЛ
ЃЈ2ЃЉЕБ![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЪБЃЌМЧКЏЪ§
ЃЉЪБЃЌМЧКЏЪ§![]() ЕФзюДѓжЕгызюаЁжЕЗж
ЕФзюДѓжЕгызюаЁжЕЗж
Б№ЮЊ![]() гы
гы![]() ЃЌЩш
ЃЌЩш![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() ЕФНт
ЕФНт
ЮіЪНЃЛ
ЃЈ3ЃЉдкЕкЃЈ2ЃЉЮЪЕФЧАЬсЯТЃЌвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЌШєЖдгкШЮвт
ЃЌШєЖдгкШЮвт![]() ЃЌ
ЃЌ ![]() ЃЌзмДцдк
ЃЌзмДцдк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]()
![]() ГЩСЂЃЌЧѓЪЕЪ§tЕФШЁжЕЗЖЮЇ.
ГЩСЂЃЌЧѓЪЕЪ§tЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫВЮМгЪІДѓИНжаЕк30НьЬяОЖдЫЖЏЛсЕФПЊФЛЪНЃЌИпШ§ФъМЖФГ6ИіАрСЊКЯЕНМЏЪаЙКТђСЫ6ИљжёИЭЃЌзїЮЊАрЦкЕФЦьИЫжЎгУЃЌЫќУЧЕФГЄЖШЗжБ№ЮЊ3.8,4.3,3.6,4.5,4.0,4.1ЃЈЕЅЮЛЃКУзЃЉЃЎ
ЃЈ1ЃЉШєДгжаЫцЛњГщШЁСНИљжёИЭЃЌЧѓГЄЖШжЎВюВЛГЌЙ§0.5УзЕФИХТЪЃЛ
ЃЈ2ЃЉШєГЄЖШВЛаЁгк4УзЕФжёИЭМлИёЮЊУПИљ10дЊЃЌГЄЖШаЁгк4УзЕФжёИЭМлИёЮЊУПИљ![]() дЊЃЎДгет6ИљжёИЭжаЫцЛњГщШЁСНИљЃЌШєЦкЭћетСНИљжёИЭЕФМлИёжЎКЭЮЊ18дЊЃЌЧѓ
дЊЃЎДгет6ИљжёИЭжаЫцЛњГщШЁСНИљЃЌШєЦкЭћетСНИљжёИЭЕФМлИёжЎКЭЮЊ18дЊЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК ![]() ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ
ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌЕу
ЃЌЕу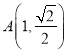 дкЭждВ
дкЭждВ![]() ЩЯЃЎ
ЩЯЃЎ
ЃЈЂёЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈЂђЃЉЪЧЗёДцдкаБТЪЮЊ2ЕФжБЯп![]() ЃЌЪЙЕУЕБжБЯп
ЃЌЪЙЕУЕБжБЯп![]() гыЭждВ
гыЭждВ![]() гаСНИіВЛЭЌНЛЕу
гаСНИіВЛЭЌНЛЕу![]() ЁЂ
ЁЂ![]() ЪБЃЌФмдкжБЯп
ЪБЃЌФмдкжБЯп![]() ЩЯевЕНвЛЕу
ЩЯевЕНвЛЕу![]() ЃЌдкЭждВ
ЃЌдкЭждВ![]() ЩЯевЕНвЛЕу
ЩЯевЕНвЛЕу![]() ЃЌТњзу
ЃЌТњзу![]() ЃПШєДцдкЃЌЧѓГіжБЯп
ЃПШєДцдкЃЌЧѓГіжБЯп![]() ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж14ЗжЃЉБОЬтЙВга2ИіаЁЬтЃЌЕк1аЁЬтТњЗж6ЗжЃЌЕк2аЁЬтТњЗж8Зж
ЩГТЉЪЧЙХДњЕФвЛжжМЦЪБзАжУЃЌЫќгЩСНИіаЮзДЭъШЋЯрЭЌЕФШнЦїКЭвЛИіЯСеЕФСЌНгЙмЕРзщГЩЃЌПЊЪМЪБЯИЩГШЋВПдкЩЯВПШнЦїжаЃЌЯИЩГЭЈЙ§СЌНгЙмЕРШЋВПСїЕНЯТВПШнЦїЫљашвЊЕФЪБМфГЦЮЊИУЩГТЉЕФвЛИіЩГЪБЁЃШчЭМЃЌФГЩГТЉгЩЩЯЯТСНИідВзЖзщГЩЃЌдВзЖЕФЕзУцжБОЖКЭИпОљЮЊ8cmЃЌЯИЩГШЋВПдкЩЯВПЪБЃЌЦфИпЖШЮЊдВзЖИпЖШЕФ![]() ЃЈЯИЙмГЄЖШКіТдВЛМЦЃЉЃЎ
ЃЈЯИЙмГЄЖШКіТдВЛМЦЃЉЃЎ

ЃЈ1ЃЉШчЙћИУЩГТЉУПУыжгТЉЯТ0.02cm3ЕФЩГЃЌдђИУЩГТЉЕФвЛИіЩГЪБЮЊЖрЩйУыЃЈОЋШЗЕН1УыЃЉЃП
ЃЈ2ЃЉЯИЩГШЋВПТЉШыЯТВПКѓЃЌЧЁКУЖбГЩИівЛИЧзЁЩГТЉЕзВПЕФдВзЖаЮЩГЖбЃЌЧѓДЫзЖаЮЩГЖбЕФИпЖШЃЈОЋШЗЕН0.1cmЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4ЁЊ4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉ.вддЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉ.вддЕуЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌдВ
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌдВ![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() .
.
ЃЈЂёЃЉаДГіжБЯп![]() ЕФЦеЭЈЗНГЬКЭдВ
ЕФЦеЭЈЗНГЬКЭдВ![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈЂђЃЉШєЕу![]() ЕФжБНЧзјБъЮЊ
ЕФжБНЧзјБъЮЊ![]() ЃЌдВ
ЃЌдВ![]() гыжБЯп
гыжБЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com