Question

18．如图，在四棱锥P-ABCD中，底面ABCD为正方形，PD=AD=2，△PAC为正三角形，E为PA的中点，F为线段BC上任意一点（不含端点）．
（1）证明：平面CDE⊥平面AFP；
（2）是否存在点F，使得三棱锥F-PAB体积为$\frac{2}{3}$，若存在，请确定点F的位置，若不存在，请说明理由．

Answer 1

分析 （1）利用勾股定理逆定理证明CD⊥PD，结合CD⊥AD得出CD⊥平面PAD，故CD⊥PA，又PA⊥DE得出PA⊥平面CDE，于是平面CDE⊥平面AFP；
（2）证明PD⊥平面ABCD，代入体积公式计算BF即可得出结论．

解答 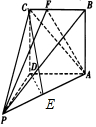（1）证明：∵PD=AD，E是PA的中点，
∴DE⊥PA．
∵PD=CD=2，PC=AC=2$\sqrt{2}$，
∴CD⊥PD，又CD⊥AD，PD∩AD=D，
∴CD⊥平面PAD，∵PA?平面PAD，
∴CD⊥PA，
又CD∩DE=D，
∴PA⊥平面CDE，
∵PA?平面APF，
∴平面CDE⊥平面AFP．
（2）解：由（1）可知PD⊥CD，同理可得PD⊥AD，
又CD∩AD=D，
∴PD⊥平面ABCD．
∴V_F-PAB=V_P-ABF=$\frac{1}{3}×\frac{1}{2}×AB×BF×PD$=$\frac{2}{3}$，
即$\frac{1}{3}×\frac{1}{2}×2×BF×2$=$\frac{2}{3}$，解得BF=1．
∴F是BC的中点．

点评 本题考查了面面垂直的判定，棱锥的体积计算，属于中档题．