
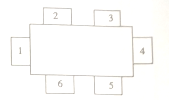
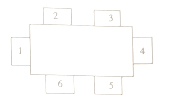
【题目】在一次体育兴趣小组的聚会中,要安排![]() 人的座位,使他们在如图所示的
人的座位,使他们在如图所示的![]() 个椅子中就坐,且相邻座位(如
个椅子中就坐,且相邻座位(如![]() 与
与![]() ,
, ![]() 与
与![]() )上的人要有共同的体育兴趣爱好.现已知这
)上的人要有共同的体育兴趣爱好.现已知这![]() 人的体育兴趣爱好如下表所示,且小林坐在
人的体育兴趣爱好如下表所示,且小林坐在![]() 号位置上,则
号位置上,则![]() 号位置上坐的是( )
号位置上坐的是( )
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |
A. 小方 B. 小张 C. 小周 D. 小马
【答案】A
【解析】重新整理,篮球:小林,小马; 网球:小林,小张;
羽毛球:小林,小李; 足球:小方,小张;
排球:小方,小李; 跆拳道:小方,小周;
棒球:小马,小李; 击剑:小周,小张
乒乓球:小马; 自行车:小周
由于小周的自行车与小马的乒乓球没有共同兴趣爱好者,所以小周两边一事实上是跆拳道与击剑的,小马两边只能是棒球与篮球的。即小马与小林一定相邻,所以1号位是小林,2 号位一定是小马,3号位就是棒球的小李。小周与小张及小方一定相邻,所以小周坐5号位。
从3号位角度,4号位只能是排球和羽毛球(小林,不可能),所以是排球小方。6号位小张。选A.
1 | 2 | 3 | 4 | 5 | 6 | 1 |
小林 | 小马 | 小李 | 小方 | 小周 | 小张 | 小林 |
/篮球 | 篮球/棒球 | 棒球/排球 | 排球/跆拳道 | 跆拳道/击剑 | 击剑/网球 | 网球 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某市对创“市级优质学校”的甲、乙两所学校复查验收,对办学的社会满意度一项评价随机访问了![]() 位市民,根据这
位市民,根据这![]() 位市民对这两所学校的评分(评分越高表明市民的评价越好),绘制茎叶图如下:
位市民对这两所学校的评分(评分越高表明市民的评价越好),绘制茎叶图如下:
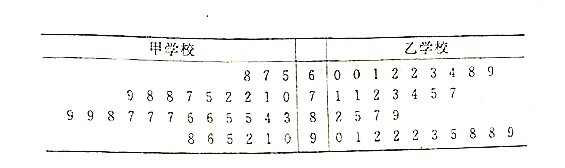
(1)分别估计该市的市民对甲、乙两所学校评分的中位数;
(2)分别估计该市的市民对甲、乙两所学校的评分不低于![]() 分的概率;
分的概率;
(3)根据茎叶图分析该市的市民对甲、乙两所学校的评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥的侧棱PD⊥底面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD= ![]() CD=2,点M在侧棱上.
CD=2,点M在侧棱上.
(1)求证:BC⊥平面BDP;
(2)若侧棱PC与底面ABCD所成角的正切值为 ![]() ,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值.
,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值. 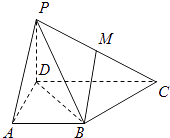
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,A,B两点5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.现记从中任取三条线且在单位时间内都通过的最大信息总量为ξ,则P(ξ≥8)= . 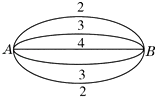
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
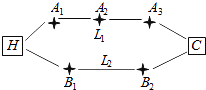
【题目】如图,李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为 ![]() ;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为 ![]() ,
, ![]() .
. 
(1)若走L1路线,求最多遇到1次红灯的概率;
(2)若走L2路线,求遇到红灯次数X的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣5:不等式选讲)
已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)设a>﹣1,且当 ![]() 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C1上,A1D⊥B1C.求证: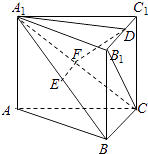
(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com