
【题目】某市对创“市级优质学校”的甲、乙两所学校复查验收,对办学的社会满意度一项评价随机访问了![]() 位市民,根据这
位市民,根据这![]() 位市民对这两所学校的评分(评分越高表明市民的评价越好),绘制茎叶图如下:
位市民对这两所学校的评分(评分越高表明市民的评价越好),绘制茎叶图如下:
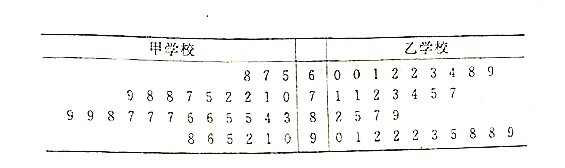
(1)分别估计该市的市民对甲、乙两所学校评分的中位数;
(2)分别估计该市的市民对甲、乙两所学校的评分不低于![]() 分的概率;
分的概率;
(3)根据茎叶图分析该市的市民对甲、乙两所学校的评价.
【答案】(1)76;(2)![]() ;(3)见解析
;(3)见解析
【解析】试题分析:(1)根据茎叶图的知识,中位数是指中间的一个或两个的平均数,首先要排序,然后再找;(2)利用样本来估计总体,只要求出样本的概率就可以了;
(3)根据(1)(2)的结果和茎叶图,合理的评价,恰当的描述即可.
试题解析:(1)由题意,根据所给的茎叶图知, ![]() 位市民对甲学校的评分按由低到高排序,排在第
位市民对甲学校的评分按由低到高排序,排在第![]() ,
, ![]() 两位的分数是
两位的分数是![]() ,
, ![]() ,故样本中位数是
,故样本中位数是![]() ,所以该市的市民对甲学校评分的中位数的估计值是
,所以该市的市民对甲学校评分的中位数的估计值是![]() .
.
![]() 位市民对乙学校的评分按由低到高排序,排在第
位市民对乙学校的评分按由低到高排序,排在第![]() ,
, ![]() 两位的分数是
两位的分数是![]() ,
, ![]() ,故样本中位数是
,故样本中位数是![]() ,所以该市的市民对乙学校评分的中位数的估计值是
,所以该市的市民对乙学校评分的中位数的估计值是![]() .
.
(2)由所给的茎叶图知, ![]() 位市民对甲、乙两学校的评分不低于
位市民对甲、乙两学校的评分不低于![]() 分的比率分别为
分的比率分别为![]() ,
, ![]() .故该市的市民对甲、乙两学校的评分不低于
.故该市的市民对甲、乙两学校的评分不低于![]() 分的概率估计值分别为
分的概率估计值分别为![]() ,
, ![]() .
.
(3)由所给茎叶图知,该市市民对甲学校的评分的中位数高于对乙学校的评分的中位数,而且由茎叶图可以大致看出市民对甲学校的评分标准差要小于对乙学校的评分的标准差,说明该市的市民对甲学校的评价较高、评价较为一致,对乙学校的评价较低、评价差异较大.


科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,两个焦点分别为
,两个焦点分别为![]() ,
, ![]() ,四边形
,四边形![]() 的面积是四边形
的面积是四边形![]() 的面积的2倍.
的面积的2倍.
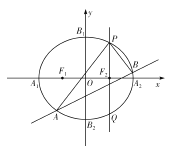
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点且垂直于
的右焦点且垂直于![]() 轴的直线交椭圆
轴的直线交椭圆![]() 于
于![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的两点.若
两侧的两点.若![]() ,求证:直线
,求证:直线![]() 的斜率
的斜率![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB= ![]() b.
b.
(Ⅰ)求角A的大小;
(Ⅱ)若a=6,b+c=8,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD.若PA=AD=AB=kBC(0<k<1),则( ) 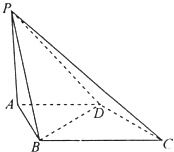
A.当k= ![]() 时,平面BPC⊥平面PCD
时,平面BPC⊥平面PCD
B.当k= ![]() 时,平面APD⊥平面PCD
时,平面APD⊥平面PCD
C.对?k∈(0,1),直线PA与底面ABCD都不垂直
D.?k∈(0,1),使直线PD与直线AC垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD的四条侧棱长相等,底面ABCD为正方形,M为PB的中点,求证:
(Ⅰ)PD∥平面ACM;
(Ⅱ)PO⊥平面ABCD;
(Ⅲ)若PA=AB,求异面直线PD与CM所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D. 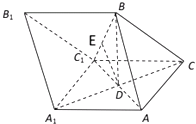
(1)求证:BD⊥A1C;
(2)若E在棱BC1上,且满足DE∥面ABC,求三棱锥E﹣ACC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
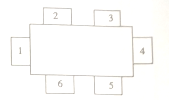
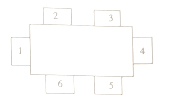
【题目】在一次体育兴趣小组的聚会中,要安排![]() 人的座位,使他们在如图所示的
人的座位,使他们在如图所示的![]() 个椅子中就坐,且相邻座位(如
个椅子中就坐,且相邻座位(如![]() 与
与![]() ,
, ![]() 与
与![]() )上的人要有共同的体育兴趣爱好.现已知这
)上的人要有共同的体育兴趣爱好.现已知这![]() 人的体育兴趣爱好如下表所示,且小林坐在
人的体育兴趣爱好如下表所示,且小林坐在![]() 号位置上,则
号位置上,则![]() 号位置上坐的是( )
号位置上坐的是( )
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |
A. 小方 B. 小张 C. 小周 D. 小马
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com