
分析 根据函数y=f(x)与函数y=-f(x)的图象关于直线x轴对称,函数y=f(x)与函数y=f(-x)的图象关于直线y轴对称,函数y=f(x)与函数y=-f(-x)的图象关于原点对称.即可得到答案.
解答 解:函数f(x)=1+$\frac{2}{3x}$的图象与y=g(x)的图象关于x轴对称,
则g(x)=-f(x)=-1-$\frac{2}{3x}$,
函数f(x)与y=h(x)关于原点对称,
则h(x)=-f(-x)=-1+$\frac{2}{3x}$,
故答案为:-1-$\frac{2}{3x}$,-1+$\frac{2}{3x}$,
点评 本题主要考查函数图象的对称变换,一般地,函数y=f(x)与函数y=-f(x)的图象关于直线x轴对称,函数y=f(x)与函数y=f(-x)的图象关于直线y轴对称,函数y=f(x)与函数y=-f(-x)的图象关于原点对称.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
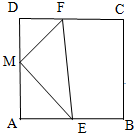 如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )| A. | $[{1,\frac{5}{4}}]$ | B. | [1,2] | C. | $[{\frac{1}{2},\frac{5}{4}}]$ | D. | $[{\frac{1}{2},\frac{3}{2}}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com