
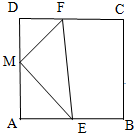
 如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )| A. | $[{1,\frac{5}{4}}]$ | B. | [1,2] | C. | $[{\frac{1}{2},\frac{5}{4}}]$ | D. | $[{\frac{1}{2},\frac{3}{2}}]$ |
分析 由题意利用两个向量垂直的条件可得ME⊥MF,设∠FMD=θ,求得$\frac{1}{2}$≤tanθ≤2,利用直角三角形中的边角关系求得△MEF的面积S=$\frac{1}{2}$•ME•MF=$\frac{1}{sin2θ}$=$\frac{1}{2}•tanθ$+$\frac{1}{2tanθ}$,令x=tanθ,再利用函数y=ax+$\frac{1}{x}$的性质,求得S(x)的范围.
解答 解:在正方形ABCD中,∵AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,∴ME⊥MF.
设∠FMD=θ,则∠EMA=90°-θ,
∵tanθ∈(0,2],且cot(90°-θ)=$\frac{1}{tanθ}$∈(0,2],∴$\frac{1}{2}$≤tanθ≤2.
∵MD=MA=1,∴△MEF的面积S=$\frac{1}{2}$•ME•MF=$\frac{1}{2}$•$\frac{MA}{cos(90°-θ)}$•$\frac{MD}{cosθ}$=$\frac{1}{sin2θ}$=$\frac{{tan}^{2}θ+1}{2tanθ}$=$\frac{1}{2}•tanθ$+$\frac{1}{2tanθ}$,
令x=tanθ,△MEF的面积S(x)=$\frac{x}{2}$+$\frac{1}{2x}$,x∈[$\frac{1}{2}$,2],
显然S(x)在[$\frac{1}{2}$,1]上是减函数,在[1,2]上是增函数,S(1)=1,
由于当x=$\frac{1}{2}$ 时,S(x)=$\frac{x}{2}$+$\frac{1}{2x}$=$\frac{5}{4}$;当 x=2时,S(x)=$\frac{5}{4}$,
故S(x)=$\frac{x}{2}$+$\frac{1}{2x}$在区间∈[$\frac{1}{2}$,2]上的最小值为1,最大值为$\frac{5}{4}$,即1≤S≤$\frac{5}{4}$,
故选:A.
点评 本题主要考查两个向量垂直的条件,直角三角形中的边角关系,三角恒等变换,函数y=ax+$\frac{1}{x}$的性质,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b2f(a)<a2f(b) | B. | b2f(a)>a2f(b) | C. | a2f(a)<b2f(b) | D. | a2f(a)>b2f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,都有2x≤0或x2-2x≤0 | B. | ?x0∈R,使得2x0≥0或x02-2x0≥0 | ||
| C. | ?x0∈R,使得2x0≤0且x02-2x0≤0 | D. | ?x0∈R,使得2x0<0或x02-2x0<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com