
| A. | b2f(a)<a2f(b) | B. | b2f(a)>a2f(b) | C. | a2f(a)<b2f(b) | D. | a2f(a)>b2f(b) |
分析 构造函数g(x)=$\frac{f(x)}{{x}^{2}}$,x∈(0,+∞),利用导数研究其单调性即可得出.
解答 解:令g(x)=$\frac{f(x)}{{x}^{2}}$,x∈(0,+∞),
g′(x)=$\frac{xf′(x)-2f(x)}{{x}^{3}}$,
∵?x∈(0,+∞),2f(x)<xf′(x)恒成立,
∴g′(x)>0,
∴函数g(x)在x∈(0,+∞)上单调递增,
∴g(a)>g(b),即$\frac{f(a)}{{a}^{2}}$>$\frac{f(b)}{{b}^{2}}$,
∴b2f(a)>a2f(b),
故选:B.
点评 本题考查了利用导数研究其单调性极值与最值、构造函数法,考查了推理能力与计算能力,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | M?N | C. | M=N | D. | M?N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{2}{3}$,+∞) | B. | (-∞,-$\frac{2}{3}$) | C. | (-$\frac{2}{3}$,0) | D. | (-1,-$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
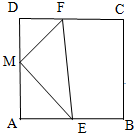 如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )
如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且$\overrightarrow{ME}•\overrightarrow{MF}$=0,则△MEF的面积的取值范围为( )| A. | $[{1,\frac{5}{4}}]$ | B. | [1,2] | C. | $[{\frac{1}{2},\frac{5}{4}}]$ | D. | $[{\frac{1}{2},\frac{3}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
| A. | y=12+3sin$\frac{πt}{6}$,t∈[0,24] | B. | y=12+3sin($\frac{πt}{6}$+π),t∈[0,24] | ||
| C. | y=12+3sin$\frac{πt}{12}$,t∈[0,24] | D. | y=12+3sin($\frac{πt}{12}$+$\frac{π}{2}$),t∈[0,24] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com