
| A. | [1,+∞) | B. | [1,e-1] | C. | (-∞,e-1] | D. | [1,$\frac{1}{2}$+ln2] |
分析 由已知得到ln$\frac{y}{x}$=$ln\frac{y}{z}•\frac{z}{x}=ln\frac{y}{z}+ln\frac{z}{x}=\frac{x}{z}+ln\frac{z}{x}$,求出$\frac{z}{x}$的范围,利用函数求导求最值.
解答 解:由正实数x,y,z满足$\frac{z}{2}$≤x≤ez且zln$\frac{y}{z}$=x,得到$\frac{1}{2}≤$$\frac{x}{z}≤e$,$ln\frac{y}{z}=\frac{x}{z}$∈[$\frac{1}{2}$,e],
ln$\frac{y}{x}$=$ln\frac{y}{z}•\frac{z}{x}=ln\frac{y}{z}+ln\frac{z}{x}=\frac{x}{z}+ln\frac{z}{x}$,
设t=$\frac{z}{x}$,则$ln\frac{y}{x}=f(t)=\frac{1}{t}+lnt$,t∈[$\frac{1}{e}$,2],
f'(t)=$-\frac{1}{{t}^{2}}+\frac{1}{t}=\frac{t-1}{{t}^{2}}$,令f'(t)=0,得到t=1,
所以当$\frac{1}{e}≤t≤1$时,f'(t)<0,函数f(t)单调递减;当1<t≤2时,函数f(t)单调递增;
当t=1时函数的最小值为f(1)=1+ln1=1;
又f(2)=$\frac{1}{2}$+ln2,f($\frac{1}{e}$)=e-1,.
又f($\frac{1}{e}$)-f(2)=e-ln2-$\frac{3}{2}$>e-lne-$\frac{3}{2}$=e-2.5>0,
所以f($\frac{1}{e}$)>f(2),
所以ln$\frac{y}{x}$的取值范围为[1,e-1];
故选B.
点评 本题考查了利用函数的思想求范围问题;关键是将所求转化为已知自变量范围的函数解析式,利用求导得到最值.属于难题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间(0,1)内有零点,在区间(1,+∞)内无零点 | |
| B. | 在区间(0,1)内有零点,在区间(1,+∞)内有零点 | |
| C. | 在区间(0,3),(3,+∞)均无零点 | |
| D. | 在区间(0,3),(3,+∞)均有零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4+2\sqrt{2}$ | B. | $4-2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
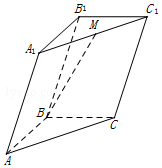
| A. | $-\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | C. | $-\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ | D. | $\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥γ,β⊥γ,则α∥β | B. | 若l1∥α,l1⊥β,则α∥β | ||
| C. | 若α∥β,l1∥α,l2∥β,则l1∥l2 | D. | 若α⊥β,l1⊥α,l2⊥β,则l1⊥l2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com