
分析 根据集合的基本运算结合一元二次方程根与系数之间的关系进行求解即可.
解答 解:∵A∩B={$\frac{1}{2}$},
∴$\frac{1}{2}$是方程2x2=sx-r和6x2+(s+2)x+r=0的公共根,
则$\frac{1}{2}$s-r=2×($\frac{1}{2}$)2,6×($\frac{1}{2}$)2+$\frac{1}{2}$(s+2)+r=0,
即s-2r=1且s+2r+5=0,
解得s=-2,r=-$\frac{3}{2}$,
则A={x|2x2=-2x+$\frac{3}{2}$}={x|4x2+4x-3=0}={$\frac{1}{2}$,-$\frac{3}{2}$},
B={x|6x2-$\frac{3}{2}$=0}={$\frac{1}{2}$,-$\frac{1}{2}$},
则A∪B={$\frac{1}{2}$,$\frac{1}{2}$,-$\frac{3}{2}$}.
点评 本题主要考查集合的基本运算,根据根与方程之间的关系是解决本题的关键.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
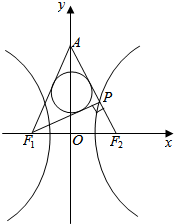 如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.
如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com