
分析 把方程f(x)=kx+k+1的根转化为函数f(x)的图象和y=kx+k+1的图象的交点在同一坐标系内画出图象由图可得结论.
解答 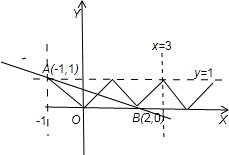 解:因为关于x的方程f(x)=kx+k+1(k∈R且k≠-1)有4个不同的根,
解:因为关于x的方程f(x)=kx+k+1(k∈R且k≠-1)有4个不同的根,
就是函数f(x)的图象与y=kx+k+1的图象有4个不同的交点,
f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=x,
所以可以得到函数f(x)的图象,
又因为y=kx+k+1=k(x+1)+1过定点(-1,1),
在同一坐标系内画出它们的图象如图,
由图得y=kx+k+1=k(x+1)+1在直线AB和y=1中间时符合要求,
而KAB=-$\frac{1}{3}$,
所以k的取值范围是:-$\frac{1}{3}$<k<0
故答案为:$(-\frac{1}{3},0)$.
点评 本题考查根的个数的应用和数形结合思想的应用.数形结合的应用大致分两类:一是以形解数,即借助数的精确性,深刻性来讲述形的某些属性;二是以形辅数,即借助与形的直观性,形象性来揭示数之间的某种关系,用形作为探究解题途径,获得问题结果的重要工具.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{77}$ | B. | 40 | C. | $\frac{1}{40}$ | D. | $\frac{1}{39}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | -15 | C. | -20 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{{\sqrt{5}}}{5}$,1) | B. | (0,$\frac{\sqrt{5}}{5}$) | C. | $(\frac{{\sqrt{3}}}{3}\;,\;\;1)$ | D. | $(0\;,\;\;\frac{{\sqrt{3}}}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com