

分析 (1)由E、F分别是AC、BC的中点,得EF∥AB,由此证明AB∥平面DEF;
(Ⅱ)以点D为坐标原点,以直线DB、DC、DA分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法找出在线段BC上存在点P,使AP⊥DE.
解答 解:(1)证明:如图(2),在△ABC中,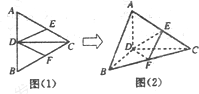
∵E、F分别是AC、BC的中点,∴EF∥AB,
又AB?平面DEF,EF?平面DEF,
∴AB∥平面DEF;
(2)以点D为坐标原点,以直线DB、DC、DA分别为x轴、y轴、z轴,
建立空间直角坐标系,如图(3)所示; 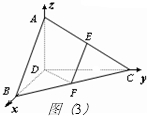
则A(0,0,2),B(2,0,0),C(0,2$\sqrt{3}$,0),
E(0,$\sqrt{3}$,1),F(1,$\sqrt{3}$,0),
$\overrightarrow{AB}$=(2,0,-2),$\overrightarrow{BC}$=(-2,2$\sqrt{3}$,0),
$\overrightarrow{DE}$=(0,$\sqrt{3}$,1),$\overrightarrow{DF}$=(1,$\sqrt{3}$,0);
设$\overrightarrow{BP}$=λ$\overrightarrow{BC}$,则$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=(2-2λ,2$\sqrt{3}$λ,-2),
由AP⊥DE得$\overrightarrow{AP}$•$\overrightarrow{DE}$=0,
∴$\sqrt{3}$×2$\sqrt{3}$λ+1×(-2)=0,解得λ=$\frac{1}{3}$,
∴在线段BC上存在点P,使AP⊥DE,且$\frac{BP}{BC}$=$\frac{1}{3}$.
点评 本题考查了直线与平面平行的证明与满足条件的点是否存在的判断问题,阶梯式要注意向量法的合理运用.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com