
| A. | -$\frac{12}{5}$ | B. | $\frac{12}{5}$ | C. | -$\frac{4}{3}$ | D. | $\frac{4}{3}$ |
分析 由题意,当($\overrightarrow{a}+\overrightarrow{b}$)$⊥\overrightarrow{b}$时,对于任意实数x,不等式|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|恒成立,此时tanθ=$\frac{1}{2}$,由此能求出tan2θ.
解答 解:由平面向量加法的几何意义,只有当($\overrightarrow{a}+\overrightarrow{b}$)$⊥\overrightarrow{b}$时,对于任意实数x,不等式|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|恒成立,如图所示,
设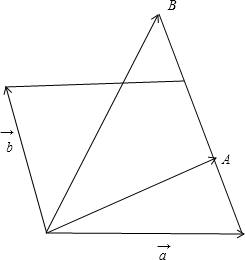 $\overrightarrow{a}+x\overrightarrow{b}=\overrightarrow{OA}$或$\overrightarrow{a}+x\overrightarrow{b}=\overrightarrow{OB}$,
$\overrightarrow{a}+x\overrightarrow{b}=\overrightarrow{OA}$或$\overrightarrow{a}+x\overrightarrow{b}=\overrightarrow{OB}$,
斜边大于直角边恒成立,
则不等式|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|恒成立,
∵向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{5}$,|$\overrightarrow{b}$|=1,
∴tanθ=-2,
∴tan2θ=$\frac{-4}{1-4}=\frac{4}{3}$.
故选:D.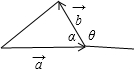 另:将不等式|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|两边平方得到不等式|$\overrightarrow{a}$+x$\overrightarrow{b}$|2≥|$\overrightarrow{a}$+$\overrightarrow{b}$|2,展开整理得得,${x}^{2}+2\sqrt{5}cosθ×x-2\sqrt{5}cosθ-1≥0$恒成立,
另:将不等式|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|两边平方得到不等式|$\overrightarrow{a}$+x$\overrightarrow{b}$|2≥|$\overrightarrow{a}$+$\overrightarrow{b}$|2,展开整理得得,${x}^{2}+2\sqrt{5}cosθ×x-2\sqrt{5}cosθ-1≥0$恒成立,
所以判别式$△=20co{s}^{2}θ{\;}^{\;}+8\sqrt{5}cosθ+4≤0$,解得cosθ=$-\frac{\sqrt{5}}{5}$,sinθ=$\frac{2\sqrt{5}}{5}$,所以tanθ=-2,tan2θ=$\frac{4}{3}$;
故选D.
点评 本题考查tan2θ的求法,是中档题,解题时要认真审题,注意向量知识和数形结合思想的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
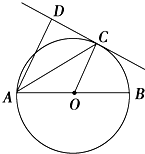 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任何一个算法一定含有顺序结构 | |
| B. | 一个算法可能同时含有顺序结构、条件结构、循环结构 | |
| C. | 循环结构中一定包含条件结构 | |
| D. | 条件结构中一定包含循环结构 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 6 | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com