Question

18．如图，在正方体ABCD-A₁B₁C₁D₁中，若M是线段A₁C₁上的动点，则下列结论不正确的是（　　）

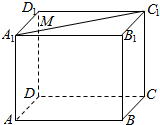
• A． 三棱锥M-ABD的主视图面积不变
• B． 三棱锥M-ABD的侧视图面积不变
• C． 异面直线CM，BD所成的角恒为$\frac{π}{2}$
• D． 异面直线CM，AB所成的角可为$\frac{π}{4}$

Answer 1

分析 判断主视图和侧视图的底与高是否发生变化来判断A，B，建立空间坐标系求出数量积来判断C和D．

解答 解：对于A，三棱锥M-ABD的主视图为三角形，底边为AB的长，高为正方体的高，故棱锥的主视图面积不变，故A正确；
对于B，侧视图为三角形的底边为AD的长，高为正方体的高，故棱锥侧视图的面积不变，故B正确；
对于C，连结AC，BD，A₁C，则BD⊥AC，∵AC∥A₁C₁，∴BD⊥A₁C₁，
又∵BD⊥CC₁，于是BD⊥平面A₁C₁C，∵CM?平面A₁C₁C，∴BD⊥CM，故C正确；
对于D，分别以AB，AD，AA₁为坐标轴，以A为原点建立空间直角坐标系，设正方体边长为1，M（a，a，1），B（1，0，0），A（0，0，0），C（1，1，0）．
∴$\overrightarrow{CM}$=（a-1，a-1，1），$\overrightarrow{AB}$=（1，0，0），∴cos＜$\overrightarrow{CM}，\overrightarrow{AB}$＞=$\frac{a-1}{\sqrt{2（a-1）^{2}+1}}$≠±$\frac{\sqrt{2}}{2}$，
∴异面直线CM，AB所成的角不可能是$\frac{π}{4}$．故D错误．
故选：D．

点评 本题考查了棱锥的三视图，异面直线所成的角，使用向量法可快速计算空间角的问题．