
分析 (Ⅰ)设袋中白球个数为x,由对立事件概率计算公式得:1-$\frac{{C}_{10-x}^{2}}{{C}_{10}^{2}}$=$\frac{7}{9}$,由此能求出白球个数.
(ii)随机变量ξ的取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量ξ的数学期望Eξ
(Ⅱ)设袋中有n个球,其中y个黑球,由题意,得y=$\frac{2}{5}$n,从而2y<n,2y≤n-1,进而$\frac{y}{n-1}≤\frac{1}{2}$,由此能证明从袋中任意摸出2个球,至少得到1个黑球的概率不大于$\frac{7}{10}$.并得到袋中哪种颜色的球个数最少.
解答 解:(Ⅰ)(i)记“从袋中任意摸出2个球,至少得到1个白球”为事件A,
设袋中白球个数为x,则P(A)=1-$\frac{{C}_{10-x}^{2}}{{C}_{10}^{2}}$=$\frac{7}{9}$,
解得x=5,∴白球个数是5个.
(ii)随机变量ξ的取值为0,1,2,3,
P(ξ=0)=$\frac{{C}_{5}^{3}}{{C}_{10}^{3}}$=$\frac{10}{120}$=$\frac{1}{12}$,
P(ξ=1)=$\frac{{C}_{5}^{1}{C}_{5}^{2}}{{C}_{10}^{3}}$=$\frac{50}{120}=\frac{5}{12}$,
P(ξ=2)=$\frac{{C}_{5}^{2}{C}_{5}^{1}}{{C}_{10}^{3}}=\frac{50}{120}=\frac{5}{12}$,
P(ξ=3)=$\frac{{C}_{5}^{3}}{{C}_{10}^{3}}$=$\frac{10}{120}=\frac{1}{12}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{5}{12}$ | $\frac{5}{12}$ | $\frac{1}{12}$ |
点评 本题考查排列组合、对立事件、相互独立事件的概率和随机变量分布列和数学期望等概念,同时考查学生的逻辑思维能力和分析问题及解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | {1,-1} | B. | {3,-3} | C. | {1,-1,3,-3} | D. | {5,-5,3,-3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
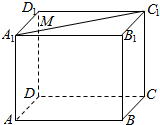
| A. | 三棱锥M-ABD的主视图面积不变 | B. | 三棱锥M-ABD的侧视图面积不变 | ||
| C. | 异面直线CM,BD所成的角恒为$\frac{π}{2}$ | D. | 异面直线CM,AB所成的角可为$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com