Question

5．如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=$\frac{1}{2}$AD，∠BAD=∠ABC=90°，E是PD的中点．
（Ⅰ）证明：直线CE∥平面PAB；
（Ⅱ）点M为棱PC 的中点，求二面角M-AB-D的余弦值．

Answer 1

分析 （Ⅰ）取PA的中点F，连接EF，BF，只需证明BCEF是平行四边形，可得CE∥BF，即可得直线CE∥平面PAB；
（Ⅱ） 取AD的中点O，M在底面ABCD上的射影N为OC的中点．
取AB的中点Q，连接MQ，NQ，即可得∠MQN就是二面角M-AB-D的平面角，解直角三角形MNQ即可得二面角M-AB-D的余弦值

解答 解（Ⅰ）证明：取PA的中点F，连接EF，BF，因为E是PD的中点，
所以EF∥AD且EF=AD，AB=BC=$\frac{1}{2}$AD，∠BAD=∠ABC=90°，∴BC∥$\frac{1}{2}$AD，
∴BCEF是平行四边形，可得CE∥BF，BF?平面PAB，CF?平面PAB，
∴直线CE∥平面PAB；
（Ⅱ）解：四棱锥P-ABCD中，
侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=$\frac{1}{2}$AD，
∠BAD=∠ABC=90°，E是PD的中点．
取AD的中点O，M在底面ABCD上的射影N为OC的中点．
取AB的中点Q，连接MQ，NQ
设AD=2，则AB=BC=1，OP=$\sqrt{3}$，
所以∠MQN就是二面角M-AB-D的平面角．
由在直角三角形MNQ中，$MN=\frac{1}{2}PO=\frac{{\sqrt{3}}}{2}，NQ=1，MQ=\sqrt{{1^2}+{{（{\frac{{\sqrt{3}}}{2}}）}^2}}=\frac{{\sqrt{7}}}{2}$
二面角M-AB-D的余弦值为：$\frac{NQ}{MQ}=\frac{1}{{\frac{{\sqrt{7}}}{2}}}=\frac{{2\sqrt{7}}}{7}$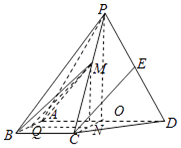

点评 本题考查了线面平行的判定，几何法求二面角，属于中档题．