
| A. | 4 | B. | 5 | C. | $\frac{4}{5}$ | D. | 与点P的位置有关 |
分析 设P(m,n),则$\frac{{n}^{2}}{4}$-n2=1,即m2-4n2=4,求出渐近线方程,求得交点A,B,再求向量PA,PB的坐标,由向量的模,计算即可得到.
解答 解:设P(m,n),则$\frac{{n}^{2}}{4}$-m2=1,即n2-4m2=4,
由双曲线$\frac{{y}^{2}}{4}$-x2=1的渐近线方程为y=±2x,
则由$\left\{\begin{array}{l}{y=2x}\\{y-n=-\frac{1}{2}(x-m)}\end{array}\right.$,解得交点A($\frac{2n+m}{5}$,$\frac{4n+2m}{5}$);
由$\left\{\begin{array}{l}{y=-2x}\\{y-n=\frac{1}{2}(x-m)}\end{array}\right.$,解得交点B($\frac{m-2n}{5}$,$\frac{4n-2m}{5}$).
$\overrightarrow{PA}$=($\frac{2n-4m}{5}$,$\frac{2m-n}{5}$),$\overrightarrow{PB}$=($\frac{-4m-2n}{5}$,$\frac{-2m-n}{5}$),
则有|PA|•|PB|=$\frac{\sqrt{(m-2n)^{2}+(4n-2m)^{2}}}{5}•\frac{\sqrt{(-4m-2n)^{2}+(-2m-n)^{2}}}{5}$=$\frac{|2m-n||2m+n|}{5}$=$\frac{4}{5}$.
故选:C.
点评 本题考查双曲线的方程和性质,考查渐近线方程的运用,考查联立方程组求交点的方法,考查向量的模求法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 | |
| B. | ?α,β∈R,使cos(α+β)=cosα+cosβ | |
| C. | 向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,0),则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为2 | |
| D. | “|x|≤1”是“x≤1”的既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (-1,2] | C. | [-1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
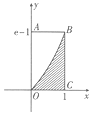 图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成,现向矩形区域OABC内随机投掷一点,则该点落在非阴影区域的概率是( )
图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成,现向矩形区域OABC内随机投掷一点,则该点落在非阴影区域的概率是( )| A. | $\frac{1}{e}$ | B. | $\frac{1}{e-1}$ | C. | 1-$\frac{1}{e}$ | D. | 1-$\frac{1}{e-1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com