
分析 (1)设事件“比赛结束时A队的得分高于B队的得分”为A,事件“比赛结束时B队的得分高于a队的得分”,事件“比赛结束时A队的得分等于B队的得分”为事件C,根据:每局比赛两队选手获胜的概率均为0.5,可得P(A)=P(B),P(A)+P(B)+P(C)=1,P(C)=0.即可得出P(A).
(2)X的可能取值为0,1,2,3,4,5.根据相互独立与互斥事件的概率计算公式即可得出.
解答 解:(1)设事件“比赛结束时A队的得分高于B队的得分”为A,事件“比赛结束时B队的得分高于a队的得分”,事件“比赛结束时A队的得分等于B队的得分”为事件C,根据:每局比赛两队选手获胜的概率均为0.5,
则P(A)=P(B),P(A)+P(B)+P(C)=1,P(C)=0.
∴P(A)=$\frac{1}{2}$.
(2)X的可能取值为0,1,2,3,4,5.
P(X=0)=$(\frac{1}{2})^{4}$=$\frac{1}{16}$,P(X=1)=$\frac{1}{2}×(1-\frac{1}{2})^{3}×3$=$\frac{3}{16}$,
P(X=2)=${∁}_{3}^{2}×(\frac{1}{2})^{2}×(1-\frac{1}{2})^{2}$+$\frac{1}{2}×(1-\frac{1}{2})^{3}$=$\frac{4}{16}$,
P(X=3)=$(\frac{1}{2})^{3}×(1-\frac{1}{2})$+$\frac{1}{2}×{∁}_{3}^{1}×\frac{1}{2}×(1-\frac{1}{2})$×$(1-\frac{1}{2})$=$\frac{4}{16}$,
P(X=4)=$\frac{1}{2}×{∁}_{3}^{2}×(\frac{1}{2})^{2}×(1-\frac{1}{2})$=$\frac{3}{16}$,P(X=5)=$(\frac{1}{2})^{4}$=$\frac{1}{16}$.
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{16}$ | $\frac{3}{16}$ | $\frac{4}{16}$ | $\frac{4}{16}$ | $\frac{3}{16}$ | $\frac{1}{16}$ |
点评 本题考查了相互独立与互斥及其对立事件的概率计算公式、随机变量的分布列与数学期望计算公式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
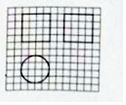 如图,网络纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三观图,切削该毛坯得到一个表面积最大的长方体,则该长方体的表面积为( )
如图,网络纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三观图,切削该毛坯得到一个表面积最大的长方体,则该长方体的表面积为( )| A. | 24 | B. | 16+32$\sqrt{2}$ | C. | 16+8$\sqrt{2}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=$\frac{1}{2}$BC=2,AC=CD=3.
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=$\frac{1}{2}$BC=2,AC=CD=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1050辆 | B. | 1350辆 | C. | 1650辆 | D. | 1950辆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | $\frac{4}{5}$ | D. | 与点P的位置有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com