
在等差数列 中,
中, ,
, ,记数列
,记数列 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)是否存在正整数 、
、 ,且
,且 ,使得
,使得 、
、 、
、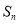 成等比数列?若存在,求出所有符合条件的
成等比数列?若存在,求出所有符合条件的 、
、 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) ;(2)
;(2)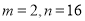 .
.
【解析】
试题分析:(1)根据等差数列的首项和公差求通项公式;(2)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的;(3)与数列有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用题中关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点.
试题解析:(1)设等差数列 的公差为
的公差为 ,
,
因为 即
即 解得
解得
所以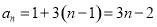 .数列
.数列 的通项为
的通项为
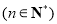 . 5分
. 5分
(2)因为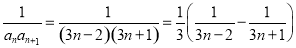 ,
,
所以数列 的前
的前 项和
项和

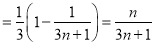 .
.
假设存在正整数 、
、 ,且
,且 ,使得
,使得 、
、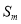 、
、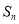 成等比数列,
成等比数列,
则 .即
.即 .
.
所以 .因为
.因为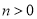 ,所以
,所以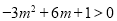 .即
.即 .
.
因为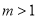 ,所以
,所以 .因为
.因为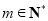 ,所以
,所以 .
.
此时 .
.
所以存在满足题意的正整数 、
、 ,且只有一组解,即
,且只有一组解,即 ,
, . 13分
. 13分
考点:(1)等差数列的通项公式;(2)裂项求和;(3)探索性问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届山东济宁任城一中高二下学期期中检测文科数学试卷(解析版) 题型:选择题
根据给出的数塔猜测123 456×9+7= ( )
1×9+2=11
12×9+3=111
123×9+4=1 111
1 234×9+5=11 111
12 345×9+6=111 111
……
A.1 111 110 B.1 111 111
C.1 111 112 D.1 111 113
查看答案和解析>>
科目:高中数学 来源:2015届山东广饶一中高二上学期期末质量检测文科数学试卷B(解析版) 题型:选择题
已知两灯塔A和B与海洋观测站C的距离相等,灯塔A在观察站C的北偏东400,灯塔B在观察站C的南偏东600,则灯塔A在灯塔B的( )
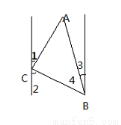
A. 北偏东100 B. 北偏西100 C. 南偏东100 D. 南偏西100
查看答案和解析>>
科目:高中数学 来源:2015届安徽省铜陵市高二下学期月考数学试卷(解析版) 题型:选择题
函数f(x)=x|x+a|+b是奇函数的充要条件是( )
A.ab=0 B.a+b=0 C.a=b D.a2+b2=0
查看答案和解析>>
科目:高中数学 来源:2015届安徽省合肥六中高二下学期期末文数学试卷(解析版) 题型:选择题
已知区域 的面积为
的面积为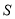 ,点集
,点集 在坐标系中对应区域的面积为
在坐标系中对应区域的面积为 ,则
,则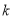 的值为( )
的值为( )
A.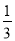 B.
B.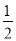 C.
C.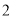 D.
D.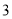
查看答案和解析>>
科目:高中数学 来源:2015届安徽师大附中高二下学期期中考查理科数学试卷(解析版) 题型:填空题
已知双曲线的两个焦点为F1(- ,0)、F2(
,0)、F2( ,0),M是此双曲线上的一点,且
,0),M是此双曲线上的一点,且 满足
满足 ·
· =0,|
=0,| |·|
|·| |=2,则该双曲线的方程是 .
|=2,则该双曲线的方程是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com