
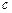 ,年产量为
,年产量为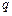 ,产品单价为
,产品单价为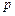 ,三者之间存在关系:
,三者之间存在关系: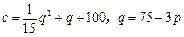 .问:应确定年产量为多少时,才能达到最大利润?此时,产品单价为多少?
.问:应确定年产量为多少时,才能达到最大利润?此时,产品单价为多少? 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源:不详 题型:解答题
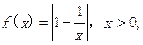
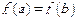 时,ab >1;
时,ab >1;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
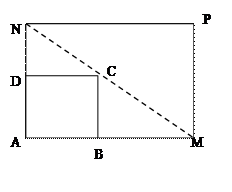 (Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省?
km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 +1上一点(-1,0),且与曲线在该点处的切线垂直的直线方程是( )
+1上一点(-1,0),且与曲线在该点处的切线垂直的直线方程是( ) +3 C y=-
+3 C y=- -
- D y=-3x-3
D y=-3x-3查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com