
���� ��1������f��n��=$\frac{2n-3}{2n+1}$f��n-1�������μ���f��2����f��3����f��4�������ݹ��ɲ���f��n����������ѧ���ɷ�֤����
��2����f��n��=$\frac{1}{16112195}$������n��ʹ��������Sn��
��� �⣺��1���������f��n��=$\frac{2n-3}{2n+1}$f��n-1����f��1��=$\frac{1}{3}$��
��f��2��=$\frac{1}{5}$f��1��=$\frac{1}{15}$��
f��3��=$\frac{3}{7}$f��2��=$\frac{1}{35}$��
f��4��=$\frac{5}{9}$f��3��=$\frac{1}{63}$��
�²⣺f��n��=$\frac{1}{��2n-1����2n+1��}$��
��Ȼn=1ʱ�����������
����n=kʱ�������������f��k��=$\frac{1}{��2k-1����2k+1��}$��
��n=k+1ʱ��f��k+1��=$\frac{2k-1}{2k+3}$f��k��=$\frac{1}{��2k+1����2k+3��}$=$\frac{1}{[2��k+1��-1][2��k+1��+1]}$��
�൱n=k+1ʱ�����������
��f��n��=$\frac{1}{��2n-1����2n+1��}$��
��2����f��n��=$\frac{1}{��2n-1����2n+1��}$=$\frac{1}{16112195}$��4n2=16112196����n=2007��
��Sn=f��1��+f��2��+f��3��+��+f��2007��=$\frac{1}{1��3}+\frac{1}{3��5}$+$\frac{1}{5��7}$+��+$\frac{1}{4013��4015}$
=$\frac{1}{2}$��1-$\frac{1}{3}$��+$\frac{1}{2}$��$\frac{1}{3}-\frac{1}{5}$��+��+$\frac{1}{2}$��$\frac{1}{4013}$-$\frac{1}{4015}$��
=$\frac{1}{2}$��1-$\frac{1}{3}+\frac{1}{3}$-$\frac{1}{5}$+��+��$\frac{1}{4013}$-$\frac{1}{4015}$��
=$\frac{1}{2}$��1-$\frac{1}{4015}$��=$\frac{2007}{4015}$��
���� ���⿼��������ͨ�ʽ����������ͣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 60�� | C�� | 60���120�� | D�� | 30���150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
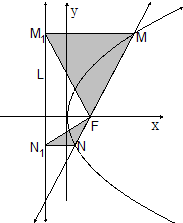 ��ֱ֪��x=my+1��������C��y2=2px��p��0���Ľ���F�����������ཻ������M��x1��y1����N��x2��y2������M��N����L�����ߣ�����ֱ�ΪM1��N1��
��ֱ֪��x=my+1��������C��y2=2px��p��0���Ľ���F�����������ཻ������M��x1��y1����N��x2��y2������M��N����L�����ߣ�����ֱ�ΪM1��N1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com