考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,分类讨论,导数的概念及应用,导数的综合应用
分析:(1)求出g(x)的导数,函数g(x)=f(x)-ax在定义域内为增函数即为g′(x)≥0,x>0恒成立,运用分离参数,运用基本不等式求得函数的最小值即可;
(2)令e
x=t,则t∈[1,2],则h(x)=H(t)=t
3-3at,求出H′(t),由H′(t)=0,得t=
,讨论①若1<t
≤,②若
<t≤2,函数的单调性,即可得到极小值;
(3)即证是否存在
x0=,使F'(x
0)=0,因为x>0时y=F'(x)单调递减,且F'(1)=0,所以即证是否存在
x0=使x
0=1.即证是否存在m,n使m=2-n.求F(x)的导数,求得单调区间,构造函数G(x)=F(x)-F(2-x),其中0<x<1,求出导数,求得单调性,运用单调性即可得证.
解答:
解:(1)g(x)=f(x)-ax=lnx+x
2-ax,g′(x)=
+2x-a
由题意,知g′(x)≥0,x>0恒成立,即a≤(2x+
)
min.
又x>0,2x+
≥2,当且仅当x=
时等号成立.
故(2x+
)
min=2
,所以a
≤2.
(2)由(Ⅰ)知,1<a
≤2,令e
x=t,则t∈[1,2],则h(x)=H(t)=t
3-3at
H′(t)=3t
2-3a=3(t-
)(t
+),由H′(t)=0,得t=
,
由于1<a
≤2,则
∈[1,
2],
①若1<t
≤,则H′(t)<0,H(t)单调递减;h(x)在(0,ln
]也单调递减;
②若
<t≤2,则H′(t)>0,H(t)单调递增.h(x)在[ln
,ln2]也单调递增;
故h(x)的极小值为h(ln
)=-2a
.
(3)即证是否存在
x0=,使F'(x
0)=0,
因为x>0时y=F'(x)单调递减,且F'(1)=0,
所以即证是否存在
x0=使x
0=1.即证是否存在m,n使m=2-n.
证明:F(x)=2lnx-x
2-k.
F′(x)=-2x=2×x、F'(x)、F(x)的变化如下:
| x | (0,1) | 1 | (1,+∞) |
| F'(x) | + | 0 | - |
| F(x) | ↗ | | ↘ |
即y=F(x)在(0,1)单调递增,在(1,+∞)单调递减.
又F(m)=F(n)=0且0<m<n所以0<m<1<n.
构造函数G(x)=F(x)-F(2-x),其中0<x<1,
即G(x)=(2lnx-x
2)-[2ln(2-x)-(2-x)
2]=2lnx-2ln(2-x)-4x+4,
G′(x)=+-4=
4×≥0,当且仅当x=1时G'(x)=0,
故y=G(x)在(0,1)单调增,所以G(x)<G(1)=0.
所以0<x<1时,F(x)<F(2-x).又0<m<1<n,
所以F(m)<F(2-m),所以F(n)=F(m)<F(2-m).
因为n、2-m∈(1,+∞),所以根据y=F(x)的单调性知n>2-m,即
>1.
又
F′(x)=-2x在(0,+∞)单调递减,所以
F′(x0)=F′()<F′(1)=0.
即函数F(x)在(x
0,F(x
0))处的切线不能平行于x轴.
点评:本题考查导数的综合应用:求切线方程和极值、最值,考查分类讨论的思想方法,以及构造函数求导数,运用单调性解题,考查运算能力,属于中档题.



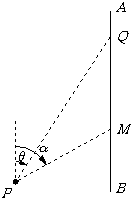 如图,P为某湖中观光岛屿,AB是沿湖岸南北方向道路,Q为停车场,PQ=
如图,P为某湖中观光岛屿,AB是沿湖岸南北方向道路,Q为停车场,PQ=