
【题目】“中国剩余定理”又称“孙子定理”.1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2019这2019个数中,能被3除余1且被4除余1的数按从小到大的顺序排成一列,构成数列![]() ,则此数列的项数为( )
,则此数列的项数为( )
A.167B.168C.169D.170
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
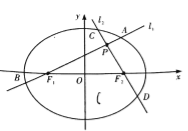
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 满足
满足![]() 且
且![]() 是它的零点,则函数
是它的零点,则函数![]() 是“有趣的”,例如
是“有趣的”,例如![]() 就是“有趣的”,已知
就是“有趣的”,已知![]() 是“有趣的”.
是“有趣的”.
(1)求出b、c并求出函数![]() 的单调区间;
的单调区间;
(2)若对于任意正数x,都有![]() 恒成立,求参数k的取值范围.
恒成立,求参数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
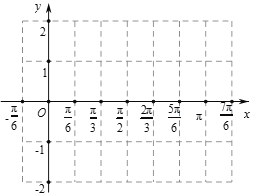
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() .若四棱锥
.若四棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积的最小值为_____;当四棱锥
的表面积的最小值为_____;当四棱锥![]() 的体积取得最大值时,二面角
的体积取得最大值时,二面角![]() 的正切值为_______.
的正切值为_______.
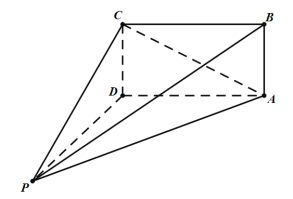
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间![]() 与数学成绩
与数学成绩![]() 进行数据收集如下:
进行数据收集如下:

由样本中样本数据求得回归直线方程为![]() ,则点
,则点![]() 与直线
与直线![]() 的位置关系是( )
的位置关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]() 与
与![]() 的大小无法确定
的大小无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学经典名著,其中有这样一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有-圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该木材,锯口深一寸,锯道长-尺.问这块圆柱形木材的直径是多少?现有长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙体中的体积约为__________立方寸.(结果保留整数)
寸,估算该木材镶嵌在墙体中的体积约为__________立方寸.(结果保留整数)
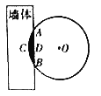
注:l丈=10尺=100寸,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
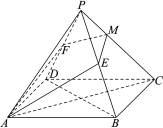
(1)求正四棱锥![]() 的全面积;
的全面积;
(2)若平面![]() 与棱
与棱![]() 交于点
交于点![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的大小(用反三角函数值表示).
所成锐二面角的大小(用反三角函数值表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com