
ЎҫМвДҝЎҝЎ¶ҫЕХВЛгКхЎ·КЗОТ№ъ№ЕҙъКэС§ҫӯөдГыЦшЈ¬ЖдЦРУРХвСщТ»ёцОКМвЈәЎ°ҪсУРФІІДЈ¬ВсФЪұЪЦРЈ¬І»ЦӘҙуРЎ.ТФҫвҫвЦ®Ј¬ЙоТ»ҙзЈ¬ҫвөАіӨТ»іЯ.ОКҫ¶јёәОЈҝЎұЖдТвОӘЈәҪсУРЈӯФІЦщРОДҫІДЈ¬ВсФЪЗҪұЪЦРЈ¬І»ЦӘЖдҙуРЎЈ¬УГҫвИҘҫвёГДҫІДЈ¬ҫвҝЪЙоТ»ҙзЈ¬ҫвөАіӨЈӯіЯ.ОКХвҝйФІЦщРОДҫІДөДЦұҫ¶КЗ¶аЙЩЈҝПЦУРіӨОӘ1ХЙөДФІЦщРОДҫІДІҝ·ЦПвЗ¶ФЪЗҪМеЦРЈ¬ҪШГжНјИзНјЛщКҫЈЁТхУ°Іҝ·ЦОӘПвЗ¶ФЪЗҪМеДЪөДІҝ·ЦЈ©.ТСЦӘПТ![]() іЯЈ¬№ӯРОёЯ
іЯЈ¬№ӯРОёЯ![]() ҙзЈ¬№АЛгёГДҫІДПвЗ¶ФЪЗҪМеЦРөДМе»эФјОӘ__________Бў·Ҫҙз.ЈЁҪб№ыұЈБфХыКэЈ©
ҙзЈ¬№АЛгёГДҫІДПвЗ¶ФЪЗҪМеЦРөДМе»эФјОӘ__________Бў·Ҫҙз.ЈЁҪб№ыұЈБфХыКэЈ©
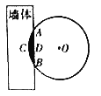
ЧўЈәlХЙЈҪ10іЯЈҪ100ҙзЈ¬![]() Ј¬
Ј¬![]() .
.

| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘөИСьМЭРО![]() ЦРЈ¬
ЦРЈ¬![]() КЗ
КЗ![]() өДЦРөгЈ¬
өДЦРөгЈ¬![]()
![]() Ј¬Ҫ«
Ј¬Ҫ«![]() СШЧЕ
СШЧЕ![]() ·ӯХЫіЙ
·ӯХЫіЙ![]() Ј¬К№ЖҪГж
Ј¬К№ЖҪГж![]() ЖҪГж
ЖҪГж![]() Ј®
Ј®


ЈЁўсЈ©ЗуЦӨЈә![]() Ј»
Ј»
ЈЁўтЈ©Зу¶юГжҪЗ![]() өДУаПТЦөЈ»
өДУаПТЦөЈ»
ЈЁўуЈ©ФЪПЯ¶О![]() ЙПКЗ·сҙжФЪөгPЈ¬К№өГ
ЙПКЗ·сҙжФЪөгPЈ¬К№өГ![]() ЖҪГж
ЖҪГж![]() Ј¬ИфҙжФЪЈ¬Зуіц
Ј¬ИфҙжФЪЈ¬Зуіц![]() өДЦөЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
өДЦөЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЛДАвЧ¶![]() ЦРЈ¬
ЦРЈ¬![]() өЧГж
өЧГж![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() КЗ
КЗ![]() өДЦРөгЈ®
өДЦРөгЈ®

ЈЁ1Ј©ЦӨГч![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() Ј¬
Ј¬
ЈЁiЈ©ЗуЦұПЯ![]() УлЖҪГж
УлЖҪГж![]() ЛщіЙҪЗөДХэПТЦөЈ»
ЛщіЙҪЗөДХэПТЦөЈ»
ЈЁiiЈ©ЙиЖҪГж![]() УлІаАв
УлІаАв![]() Ҫ»УЪ
Ҫ»УЪ![]() Ј¬Зу
Ј¬Зу![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЎ°ЦР№ъКЈУа¶ЁАнЎұУЦіЖЎ°ЛпЧУ¶ЁАнЎұ.1852ДкЈ¬Уў№ъАҙ»Әҙ«ҪМКҝО°БТСЗБҰҪ«Ў¶ЛпЧУЛгҫӯЎ·ЦРЎ°ОпІ»ЦӘКэЎұОКМвөДҪв·Ёҙ«ЦБЕ·ЦЮ.1874ДкЈ¬Уў№ъКэС§јТВнОчЙӯЦёіцҙЛ·Ё·ыәП1801ДкУЙёЯЛ№өГөҪөД№ШУЪН¬УаКҪҪв·ЁөДТ»°гРФ¶ЁАнЈ¬Тт¶шОч·ҪіЖЦ®ОӘЎ°ЦР№ъКЈУа¶ЁАнЎұ.Ў°ЦР№ъКЈУа¶ЁАнЎұҪІөДКЗТ»ёц№ШУЪХыіэөДОКМвЈ¬ПЦУРХвСщТ»ёцХыіэОКМвЈәҪ«1өҪ2019Хв2019ёцКэЦРЈ¬ДЬұ»3іэУа1ЗТұ»4іэУа1өДКэ°ҙҙУРЎөҪҙуөДЛіРтЕЕіЙТ»БРЈ¬№№іЙКэБР![]() Ј¬ФтҙЛКэБРөДПоКэОӘЈЁ Ј©
Ј¬ФтҙЛКэБРөДПоКэОӘЈЁ Ј©
A.167B.168C.169D.170
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪКөКэјҜRЦР,ОТГЗ¶ЁТеөДҙуРЎ№ШПөЎ°ЈҫЎұОӘИ«МеКөКэЕЕБЛТ»ёцЎ°РтЎұ.АаЛЖөШ,ОТГЗФЪёҙКэјҜCЙПТІҝЙТФ¶ЁТеТ»ёціЖОӘЎ°РтЎұөД№ШПө,јЗОӘЎ°ЈҫЎұ.¶ЁТеИзПВ:¶ФУЪИОТвБҪёцёҙКэЈә![]() өұЗТҪцөұЎ°
өұЗТҪцөұЎ°![]() Ўұ»тЎ°
Ўұ»тЎ°![]() ЎұЗТЎ°
ЎұЗТЎ°![]() Ўұ.°ҙЙПКц¶ЁТеөД№ШПөЎ°ЈҫЎұЈ¬ёшіцТФПВЛДёцГьМв:
Ўұ.°ҙЙПКц¶ЁТеөД№ШПөЎ°ЈҫЎұЈ¬ёшіцТФПВЛДёцГьМв:
ўЩИф![]() ,Фт
,Фт![]() Ј»
Ј»
ўЪИф![]() Ј¬Фт
Ј¬Фт![]() Ј»
Ј»
ўЫИф![]() ,Фт¶ФУЪИОТв
,Фт¶ФУЪИОТв![]() Ј»
Ј»
ўЬ¶ФУЪёҙКэ![]() ,Иф
,Иф![]() ,Фт
,Фт![]() .
.
ЖдЦРЛщУРХжГьМвөДРтәЕОӘ______________.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘДіНЦФІCЈ¬ЛьөДЦРРДФЪЧшұкФӯөгЈ¬ЧуҪ№өгОӘFЈЁ©Ғ![]() Ј¬0Ј©Ј¬ЗТ№эөгDЈЁ2Ј¬0Ј©Ј®
Ј¬0Ј©Ј¬ЗТ№эөгDЈЁ2Ј¬0Ј©Ј®
ЈЁ1Ј©ЗуНЦФІCөДұкЧј·ҪіМЈ»
ЈЁ2Ј©ИфТСЦӘөгAЈЁ1Ј¬![]() Ј©Ј¬өұөгPФЪНЦФІCЙПұд¶ҜКұЈ¬ЗуіцПЯ¶ОPAЦРөгMөД№мјЈ·ҪіМЈ®
Ј©Ј¬өұөгPФЪНЦФІCЙПұд¶ҜКұЈ¬ЗуіцПЯ¶ОPAЦРөгMөД№мјЈ·ҪіМЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() НјПуБҪМхПаБЪөД¶ФіЖЦбјдөДҫаАлОӘ
НјПуБҪМхПаБЪөД¶ФіЖЦбјдөДҫаАлОӘ![]() .
.
ЈЁ1Ј©Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©Ҫ«әҜКэ![]() өДНјПуСШ
өДНјПуСШ![]() ЦбПтЧуЖҪТЖ
ЦбПтЧуЖҪТЖ![]() ёцөҘО»іӨ¶ИәуЈ¬ФЩҪ«өГөҪөДНјПуЙПёчөгөДәбЧшұкұдОӘФӯАҙөД
ёцөҘО»іӨ¶ИәуЈ¬ФЩҪ«өГөҪөДНјПуЙПёчөгөДәбЧшұкұдОӘФӯАҙөД![]() ұ¶Ј¬ЧЭЧшұкІ»ұдЈ¬өГөҪәҜКэ
ұ¶Ј¬ЧЭЧшұкІ»ұдЈ¬өГөҪәҜКэ![]() өДНјПуЈ¬Зу
өДНјПуЈ¬Зу![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЦРРДФЪФӯөгөДНЦФІC1әНЕЧОпПЯC2УРПаН¬өДҪ№өг(1Ј¬0)Ј¬НЦФІC1№эөг![]() Ј¬ЕЧОпПЯ
Ј¬ЕЧОпПЯ![]() өД¶ҘөгОӘФӯөгЈ®
өД¶ҘөгОӘФӯөгЈ®
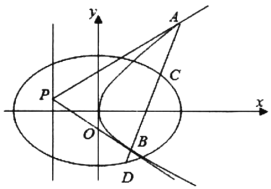
(1)ЗуНЦФІC1әНЕЧОпПЯC2өД·ҪіМЈ»
(2)ЙиөгPОӘЕЧОпПЯC2ЧјПЯЙПөДИОТвТ»өгЈ¬№эөгPЧчЕЧОпПЯC2өДБҪМхЗРПЯPAЈ¬PBЈ¬ЖдЦРAЎўBОӘЗРөгЈ®
ЙиЦұПЯPAЈ¬PBөДРұВК·ЦұрОӘk1Ј¬k2Ј¬ЗуЦӨЈәk1k2ОӘ¶ЁЦөЈ»
ўЪИфЦұПЯABҪ»НЦФІC1УЪCЈ¬DБҪөгЈ¬SЎчPABЈ¬SЎчPCD·ЦұрКЗЎчPABЈ¬ЎчPCDөДГж»эЈ¬КФОКЈә![]() КЗ·сУРЧоРЎЦө?ИфУРЈ¬ЗуіцЧоРЎЦөЈ»ИфГ»УРЈ¬ЗлЛөГчАнУЙ.
КЗ·сУРЧоРЎЦө?ИфУРЈ¬ЗуіцЧоРЎЦөЈ»ИфГ»УРЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝКҜЧмЙҪКРөЪИэЦРС§ёЯИэДкј¶НіјЖС§ЙъөДЧоҪь20ҙОКэС§ЦЬІвіЙјЁЈЁВъ·Ц150·ЦЈ©Ј¬ПЦУРјЧТТБҪО»Н¬С§өД20ҙОіЙјЁИзҫҘТ¶НјЛщКҫ:
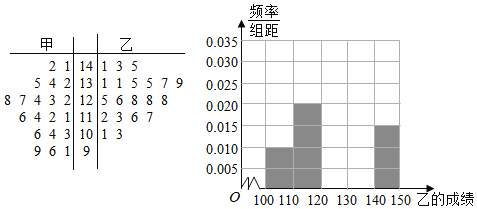
ЈЁ1Ј©ёщҫЭҫҘТ¶НјЗујЧТТБҪО»Н¬С§іЙјЁөДЦРО»КэЈ¬ІўҪ«Н¬С§ТТөДіЙјЁөДЖөВК·ЦІјЦұ·ҪНјМоідНкХыЈ»
ЈЁ2Ј©ёщҫЭҫҘТ¶НјұИҪПјЧТТБҪО»Н¬С§КэС§іЙјЁөДЖҪҫщЦөј°ОИ¶ЁіМ¶ИЈЁІ»ТӘЗујЖЛгіцҫЯМеЦөЈ¬ёшіцҪбВЫјҙҝЙЈ©Ј»
ЈЁ3Ј©ПЦҙУјЧТТБҪО»Н¬С§өДІ»өНУЪ140·ЦөДіЙјЁЦРИОТвСЎіц2ёціЙјЁЈ¬јЗКВјю![]() ОӘЎ°ЖдЦР2ёціЙјЁ·ЦұрКфУЪІ»Н¬өДН¬С§ЎұЈ¬ЗуКВјю
ОӘЎ°ЖдЦР2ёціЙјЁ·ЦұрКфУЪІ»Н¬өДН¬С§ЎұЈ¬ЗуКВјю![]() ·ўЙъөДёЕВК.
·ўЙъөДёЕВК.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com