
【题目】已知平面直角坐标系内的动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离比为
的距离比为![]() .
.
(1)求动点P所在曲线E的方程;
(2)设点Q为曲线E与![]() 轴正半轴的交点,过坐标原点O作直线
轴正半轴的交点,过坐标原点O作直线![]() ,与曲线E相交于异于点
,与曲线E相交于异于点![]() 的不同两点
的不同两点![]() ,点C满足
,点C满足![]() ,直线
,直线![]() 和
和![]() 分别与以C为圆心,
分别与以C为圆心,![]() 为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比
为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1) 设动点P的坐标为![]() , 由题意可得
, 由题意可得![]() ,整理可得曲线E的方程;
,整理可得曲线E的方程;
(2) 解法一:可得圆C方程为![]() ,设直线MQ的方程为
,设直线MQ的方程为![]() ,设直线NQ的方程为
,设直线NQ的方程为![]() ,分别与圆联立,可得
,分别与圆联立,可得![]() ,
,![]() ,可得
,可得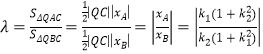 ,可得
,可得![]() ,代入可得答案;
,代入可得答案;
解法二:可得圆C方程为![]() ,设直线MQ的方程为
,设直线MQ的方程为![]() ,则点C到MQ的距离为
,则点C到MQ的距离为![]() ,
,![]()
![]() ,
,![]()
![]() ,设直线NQ的方程为
,设直线NQ的方程为![]() ,同理可得:
,同理可得:![]()
![]() ,
,![]() ,可得
,可得![]() ,代入可得答案.
,代入可得答案.
解:(1)设动点P的坐标为![]() ,由题意可得
,由题意可得![]() ,
,
整理,得:![]() ,即
,即![]() 为所求曲线E的方程;
为所求曲线E的方程;
(2)(解法一)由已知得:![]() ,
,![]() ,
,![]() ,即圆C方程为
,即圆C方程为![]()
由题意可得直线MQ,NQ的斜率存在且不为0
设直线MQ的方程为![]() ,与
,与![]() 联立得:
联立得:![]()
所以,![]()
同理,设直线NQ的方程为![]() ,与
,与![]() 联立得:
联立得:![]()
所以![]()
因此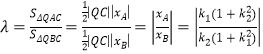
由于直线![]() 过坐标原点,所以点
过坐标原点,所以点![]() 与点
与点![]() 关于坐标原点对称
关于坐标原点对称
设![]() ,
,![]() ,所以,
,所以,![]()
又![]() 在曲线
在曲线![]() 上,所以
上,所以![]() ,即
,即![]()
故![]() ,
,
由于![]() ,所以,
,所以,![]()
(解法二)由已知得:![]() ,
,![]() ,
,![]() ,即圆C方程为
,即圆C方程为![]()
由题意可得直线MQ,NQ的斜率存在且不为0
设直线MQ的方程为![]() ,则点C到MQ的距离为
,则点C到MQ的距离为![]()
所以![]()
于是,![]()
![]()
设直线NQ的方程为![]() ,同理可得:
,同理可得:![]()
![]()
所以![]()
由于直线l过坐标原点,所以点M与点N关于坐标原点对称
设![]() ,
,![]() ,所以,
,所以,![]()
又![]() 在曲线
在曲线![]() 上,所以
上,所以![]() ,即
,即![]()
故![]() ,
,
由于![]() ,所以,
,所以,![]()


科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例。
(2)能否在犯错误的概率不超过百分之一的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保证树苗的质量,林业管理部门在每年3月12日植树节前都对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度![]() 单位长度:
单位长度:![]() ,其茎叶图如图所示,则下列描述正确的是( )
,其茎叶图如图所示,则下列描述正确的是( )
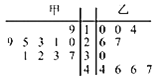
A. 甲种树苗的平均高度大于乙种树苗的平均高度,甲种树苗比乙种树苗长得整齐
B. 甲种树苗的平均高度大于乙种树苗的平均高度,乙种树苗比甲种树苗长得整齐
C. 乙种树苗的平均高度大于甲种树苗的平均高度,乙种树苗比甲种树苗长得整齐
D. 乙种树苗的平均高度大于甲种树苗的平均高度,甲种树苗比乙种树苗长得整齐
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点E是棱
中,点E是棱![]() 的中点,点F是线段
的中点,点F是线段![]() 上的一个动点.有以下三个命题:
上的一个动点.有以下三个命题:
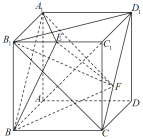
①异面直线![]() 与
与![]() 所成的角是定值;
所成的角是定值;
②三棱锥![]() 的体积是定值;
的体积是定值;
③直线![]() 与平面
与平面![]() 所成的角是定值.
所成的角是定值.
其中真命题的个数是( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种出口产品的关税税率t.市场价格x(单位:千元)与市场供应量p(单位:万件)之间近似满足关系式:![]() ,其中k.b均为常数.当关税税率为75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
,其中k.b均为常数.当关税税率为75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
(1)试确定k.b的值;
(2)市场需求量q(单位:万件)与市场价格x近似满足关系式:![]() .P = q时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率
.P = q时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,使
,使![]() 是等边三角形且面积为
是等边三角形且面积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 是圆
是圆![]() 与抛物线
与抛物线![]() 的一个交点,点
的一个交点,点![]() ,当
,当![]() 取得最小值时,求此时圆
取得最小值时,求此时圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系(
轴正半轴为极轴,建立极坐标系(![]() ),点
),点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() 。
。
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)设点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 面积的最小值。
面积的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com