
已知 ,
,
(1)对一切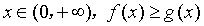 恒成立,求实数
恒成立,求实数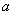 的取值范围;
的取值范围;
(2)当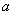 =1时,求函数
=1时,求函数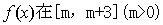 上的最小值和最大值;
上的最小值和最大值;
(3)证明:对一切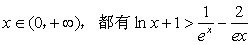 成立。
成立。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
已知命题 :“若
:“若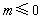 ,则
,则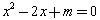 有实数解”的逆命题;命题
有实数解”的逆命题;命题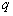 :“若函数
:“若函数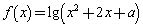 的值域为
的值域为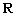 ,则
,则 ”.以下四个结论:
”.以下四个结论:
① 是真命题;②
是真命题;②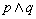 是假命题;③
是假命题;③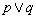 是假命题;④
是假命题;④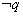 为假命题.
为假命题.
其中所有正确结论的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
在某种新型材料的研制中,实验人员获得了右边一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是
( )
|
| 1.99 | 3 | 4 | 5.1 | 6.12 |
|
| 1.5 | 4.04 | 7.5 | 12 | 18.01 |
A. 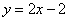 B.
B. 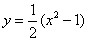
B.C.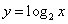 D.
D. 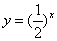
查看答案和解析>>
科目:高中数学 来源: 题型:
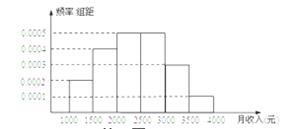
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如上图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在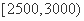 (元)月收入段应抽出
(元)月收入段应抽出
的人数为( ).
A.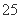 B.
B.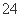 C.
C.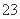 D.
D.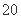
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com