
分析 根据平面向量的数量积,利用同角的三角函数关系求出tanθ的值,再化简$\frac{{2{{cos}^2}\frac{θ}{2}-sinθ-1}}{{\sqrt{2}sin(θ+\frac{π}{4})}}$并求值.
解答 解:向量$\overrightarrow a$=(1,-$\sqrt{3}$),$\overrightarrow b$=(sinx,cosx),
f(x)=$\overrightarrow a$•$\overrightarrow b$=sinx-$\sqrt{3}$cosx,
∴f(θ)=sinθ-$\sqrt{3}$cosθ=0,
∴$\frac{sinθ}{cosθ}$=tanθ=$\sqrt{3}$;
∴$\frac{{2{{cos}^2}\frac{θ}{2}-sinθ-1}}{{\sqrt{2}sin(θ+\frac{π}{4})}}$=$\frac{2•\frac{1+cosθ}{2}-sinθ-1}{\sqrt{2}(sinθcos\frac{π}{4}+cosθsin\frac{π}{4})}$
=$\frac{cosθ-sinθ}{sinθ+cosθ}$
=$\frac{1-tanθ}{tanθ+1}$
=$\frac{1-\sqrt{3}}{\sqrt{3}+1}$
=$\frac{{(1-\sqrt{3})}^{2}}{{1}^{2}{-(\sqrt{3})}^{2}}$
=$\sqrt{3}$-2.
点评 本题考查了平面向量的数量积运算和三角函数的化简求值问题,是中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | |
| C. | 若($\sqrt{x}$-$\frac{1}{2\root{3}{x}}$)n的展开式中第四项为常数项,则n=5 | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
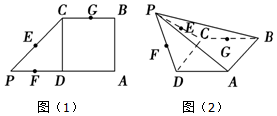 在如图(1)的平面图形中,ABCD为正方形,CDP为等腰直角三角形,E、F、G分别是PC、PD、CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD如图(2).
在如图(1)的平面图形中,ABCD为正方形,CDP为等腰直角三角形,E、F、G分别是PC、PD、CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD如图(2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{64}{15}$ | C. | $\frac{16}{19}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
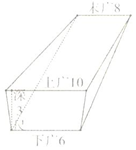 《九章算术》是东方数学思想之源,在卷五《商功》中有以下问题:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?译文:如图所示的几何体是三个侧面皆为等腰梯形,其他两面为直角三角形的五面体,(前端)下宽6尺,上宽一丈,深3尺,末端宽8尺,无深,长7尺,则它的体积是84立方尺.
《九章算术》是东方数学思想之源,在卷五《商功》中有以下问题:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?译文:如图所示的几何体是三个侧面皆为等腰梯形,其他两面为直角三角形的五面体,(前端)下宽6尺,上宽一丈,深3尺,末端宽8尺,无深,长7尺,则它的体积是84立方尺.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3,-3 | B. | 1,-3 | C. | 1,-1 | D. | 3,-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com