Question

20．直角三角形ABC中，AB=3，AC=4，BC=5，点M是三角形ABC外接圆上任意一点，则$\overrightarrow{AB}•\overrightarrow{AM}$的最大值为12．

Answer 1

分析 建立坐标系，设M （$\frac{3}{2}+\frac{5}{2}cosα，2+\frac{5}{2}sinα$），则 $\overrightarrow{AM}$=（$\frac{3}{2}+\frac{5}{2}cosα，2+\frac{5}{2}sinα$），$\overrightarrow{AB}=（3，0）$，$\overrightarrow{AB}•\overrightarrow{AM}=\frac{9}{2}+\frac{15}{2}cosα≤12$

解答 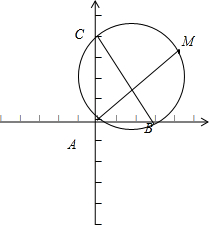解：如图建立平面直角坐标系，A（0，0），B（3，0），C（0.4），
三角形ABC外接圆（x-$\frac{3}{2}$）²+（y-2）²=$\frac{25}{4}$，
设M （$\frac{3}{2}+\frac{5}{2}cosα，2+\frac{5}{2}sinα$），则 $\overrightarrow{AM}$=（$\frac{3}{2}+\frac{5}{2}cosα，2+\frac{5}{2}sinα$），$\overrightarrow{AB}=（3，0）$，
$\overrightarrow{AB}•\overrightarrow{AM}=\frac{9}{2}+\frac{15}{2}cosα≤12$，
故答案为：12．

点评 本题考查了圆的参数方程、三角函数的单调性、数量积坐标运算，考查了推理能力与计算能力，属于中档题