
| A. | a>b>c | B. | a<b<c | C. | a<c<b | D. | b<c<a |
分析 利用二倍角公式、诱导公式化简a、b、c,再利用余弦函数的单调性,得出结论.
解答 解:∵a=$\frac{1}{2}cos6°$-$\frac{{\sqrt{3}}}{2}sin6°$=cos(60°-6°)=cos54°,
b=cos26°•$\frac{2tan13°}{{1-{{tan}^2}13°}}$=cos26°•tan26°=sin26°=cos64°,
c=$\sqrt{\frac{1-cos50°}{2}}$=sin25°=cos65°,
而函数y=cosx在(0°,180°)上单调递减,54°<64°<65°,
∴cos54°>cos64°>cos65°,即 a>b>c,
故选:A.
点评 本题主要考查二倍角公式、诱导公式的应用,余弦函数的单调性,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2017×22015 | B. | 2017×22014 | C. | 2016×22015 | D. | 2016×22014 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
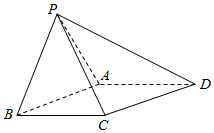 已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$
已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com