
| A. | 2017×22015 | B. | 2017×22014 | C. | 2016×22015 | D. | 2016×22014 |
分析 由题意,数表的每一行都是等差数列,且第一行公差为1,第二行公差为2,第三行公差为4,…,第2015行公差为22014,可得:第n行的第一个数为:(n+1)×2n-2,即可得出.
解答 解:由题意,数表的每一行都是等差数列,
且第一行公差为1,第二行公差为2,第三行公差为4,…,第2015行公差为22014,
故第1行的第一个数为:2×2-1,
第2行的第一个数为:3×20,
第3行的第一个数为:4×21,
…
第n行的第一个数为:(n+1)×2n-2,
第2016行只有M,
则M=(1+2016)•22014=2017×22014,
故选:B
点评 本题考查了等差和等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
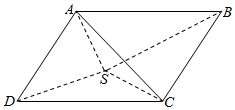 如图,四边形 A BCD为平行四边形,且SD=2,SC=DC=AS=AD=$\sqrt{2}$,平面 ASD⊥平面SDC.
如图,四边形 A BCD为平行四边形,且SD=2,SC=DC=AS=AD=$\sqrt{2}$,平面 ASD⊥平面SDC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a<b<c | C. | a<c<b | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com