
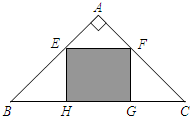
 如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )
如图,有一块等腰直角三角形ABC的空地,要在这块空地上开辟一个内接矩形EFGH的绿地,已知AB⊥AC,AB=4,绿地面积最大值为( )| A、6 | ||
B、4
| ||
| C、4 | ||
D、2
|
 如图,设AF=x,则0<x<4,∴FC=4-x,
如图,设AF=x,则0<x<4,∴FC=4-x,| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、a、b、c都是奇数 |
| B、a、b、c都是偶数 |
| C、a、b、c中至少有两个偶数 |
| D、a、b、c中或都是奇数或至少有两个偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、(-6,6)∪(
| ||
B、(
| ||
C、(-∞,-
| ||
D、(-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、x-y-1=0 |
| B、x-y-1=0或x-y-4=0 |
| C、x+y-3=0 |
| D、x-y-1=0或x=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
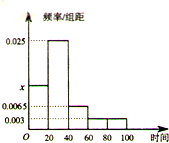 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com