
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC,则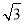 sinA-cos(B+
sinA-cos(B+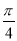 )的最大值为( )
)的最大值为( )
A.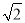 B.2
B.2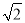 C.
C.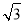 D.2
D.2
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-4数系的扩充与复数的引入(解析版) 题型:填空题
已知复数z=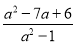 +(a2-5a-6)i(a∈R)为实数,则a=________.
+(a2-5a-6)i(a∈R)为实数,则a=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
BC是单位圆A的一条直径,F是线段AB上的点,且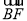 =2
=2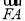 ,若DE是圆A中绕圆心A运动的一条直径,则
,若DE是圆A中绕圆心A运动的一条直径,则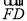 ·
·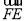 的值是( )
的值是( )
A.-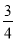 B.-
B.-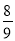 C.-
C.-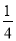 D.不确定
D.不确定
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:解答题
如图,A,B是海面上位于东西方向相距5(3+ )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?

查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
要测量底部不能到达的东方明珠电视塔的高度,在黄埔江西岸选择C、D两观测点,在C、D两点测得塔顶的仰角分别为45°,30°,在水平面上测得电视塔底与C地连线及C、D两地连线所成的角为120°,C、D两地相距500 m,则电视塔的高度是( )
A.100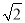 m B.400 m C.200
m B.400 m C.200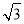 m D.500 m
m D.500 m
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:填空题
在△ABC中,a,b,c分别是角A,B,C的对边,已知cos2A-3cos(B+C)=1,若△ABC的面积S=5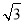 ,b=5,则c的值为________.
,b=5,则c的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
已知在锐角△ABC中,角A,B,C所对的边分别为a,b,c,且tanC=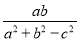 ,则角C为( )
,则角C为( )
A. B.
B.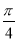 C.
C.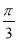 D.
D.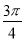
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:解答题
已知函数f(x)=6cos2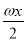 +
+ sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
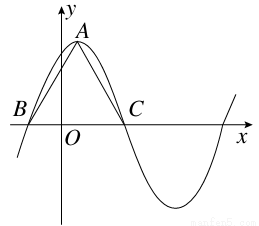
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)=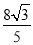 ,且x0∈(-
,且x0∈(-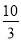 ,
,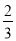 ),求f(x0+1)的值.
),求f(x0+1)的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:选择题
函数f(x)= cos(ωx+φ)对任意的x∈R,都有f(
cos(ωx+φ)对任意的x∈R,都有f(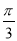 -x)=f(
-x)=f(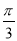 +x),若函数g(x)=3sin(ωx+φ)-2,则g(
+x),若函数g(x)=3sin(ωx+φ)-2,则g(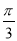 )的值是( )
)的值是( )
A.1 B.-5或3 C.-2 D.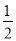
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com