
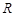 的函数
的函数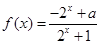 是奇函数.
是奇函数.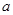 值;
值;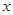 的函数
的函数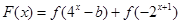 有零点,求实数
有零点,求实数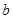 的取值范围.
的取值范围.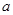 =1.(Ⅱ)f(x)在R上为减函数..(Ⅲ)
=1.(Ⅱ)f(x)在R上为减函数..(Ⅲ)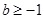 .
.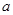 的值.(Ⅱ)已知函数式化简后计算会简单些,通过单调性的定义证明函数在R上是递减的.(Ⅲ)通过第二步的单调性可得两个变量要相等,求出b的范围.本题包含了函数的奇偶性的知识,单调性的知识,同时对单调性做了一个应用.综合性较强难度不算大.第三步的范围有一定的难度,最后转化为根的存在性所以b应该大于或等于
的值.(Ⅱ)已知函数式化简后计算会简单些,通过单调性的定义证明函数在R上是递减的.(Ⅲ)通过第二步的单调性可得两个变量要相等,求出b的范围.本题包含了函数的奇偶性的知识,单调性的知识,同时对单调性做了一个应用.综合性较强难度不算大.第三步的范围有一定的难度,最后转化为根的存在性所以b应该大于或等于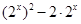 的最小值,这个解题思想要理解把握.
的最小值,这个解题思想要理解把握.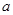 =1,经检验符合.
=1,经检验符合. ,f(x)在R上为减函数下:设在R上为减函数.
,f(x)在R上为减函数下:设在R上为减函数. 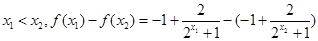
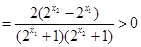 .所以f(x)在R上为减函数.
.所以f(x)在R上为减函数.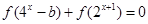 ,
,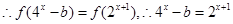 有解.所以b=
有解.所以b=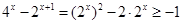


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源:不详 题型:单选题
 的图象向右平移
的图象向右平移 个单位后关于
个单位后关于 对称,当
对称,当 时,
时, <0恒成立,设
<0恒成立,设 ,
, ,
, ,则
,则 的大小关系为( )
的大小关系为( )| A.c>a>b | B.c>b>a | C.a>c>b | D.b>a>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com