
分析 (1)利用两个等式得到关于公差d是方程组解之;
(2)利用(1)的结论得到前n项和为Sn,利用裂项相消求和.
解答 解:(1)设等差数列{an}的公差为d(d>0),则由题意,b1=1,b2=8,b3=64,所以$\left\{\begin{array}{l}{8(6+d)=64}\\{64(9+3d)=640}\end{array}\right.$解得:d=2,∴an=2n+1;
(2)由(1)可得:${S_n}={n^2}+2n$
∴$\frac{1}{S_n}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$
∴$\frac{1}{S_1}+\frac{1}{S_2}+…+\frac{1}{S_n}=\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})=\frac{3}{4}-\frac{1}{2}(\frac{1}{n+1}+\frac{1}{n+2})$.
点评 本题考查了等差数列与等比数列的通项公式以及裂项相消法求数列的和;比较基础.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
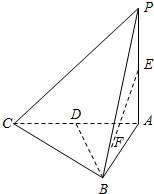 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
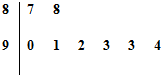 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91、5 | B. | 91、5.5 | C. | 92、5.5 | D. | 92、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,+∞) | B. | [-1,0)∪(0,+∞) | C. | (-1,+∞) | D. | [-1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com