
已知二次函数f(x)=ax2+bx+c(a≠0)且满足f(-1)=0,对任意实数x,恒有f(x)-x≥0,并且当x∈(0,2)时,有f(x)≤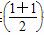 2.
2.
(1)求f(1)的值;
(2)证明a>0,c>0;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx(x∈R)是单调函数,求证:m≤0或m≥1.
(1)对x∈R,f(x)-x≥0恒成立,
当x=1时,f(1)≥1,
又∵1∈(0,2),由已知得f(1)≤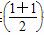 2=1,
2=1,
∴1≤f(1)≤1,∴f(1)=1.
(2)证明:∵f(1)=1,f(-1)=0,∴a+b+c=1,
a-b+c=0,∴b=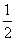 .∴a+c=
.∴a+c=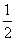 .
.
∵f(x)-x≥0对x∈R恒成立,
∴ax2-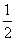 x+c≥0对x∈R恒成立,
x+c≥0对x∈R恒成立,
∴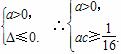 ∴c>0,故a>0,c>0.
∴c>0,故a>0,c>0.
(3)证明:∵a+c=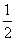 ,ac≥
,ac≥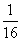 ,由a>0,c>0及a+c≥2
,由a>0,c>0及a+c≥2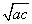 ,得ac≤
,得ac≤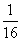 ,∴ac=
,∴ac=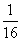 ,当且仅当a=c=
,当且仅当a=c=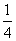 时,取“=”.
时,取“=”.
∴f(x)=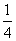 x2+
x2+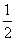 x+
x+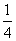 .
.
∴g(x)=f(x)-mx=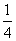 x2+
x2+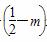 x+
x+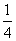 =
=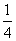 [x2+(2-4m)x+1].
[x2+(2-4m)x+1].
∵g(x)在[-1,1]上是单调函数,
∴2m-1≤-1或2m-1≥1,∴m≤0或m≥1.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
用min{a,b}表示a、b两数中的最小值,若函数f(x)=min{|x|,|x+t|}的图象关于直线x=-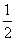 对称,则t的值为( )
对称,则t的值为( )
A.-2 B.2
C.-1 D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
给出命题:若函数y=f(x)是幂函数,则函数y=f(x)的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
A.3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知三个函数f(x)=2x+x,g(x)=x-2,h(x)=log2x+x的零点依次为a,b,c,则( )
A.a<b<c B.a<c<b
C.b<a<c D.c<a<b
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的偶函数y=f(x),当x≥0时,y=f(x)是单调递增的,f(1)·f(2)<0.则函数y=f(x)的图象与x轴的交点个数是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com